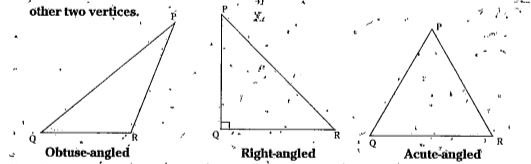
Answer
Step by step text solution for Can you think of a triangle in which the two altitudes of a triangle are two of its’sides? by MATHS experts to help you in doubts & scoring excellent marks in Class 7 exams.
|
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
Recommended Questions
- Can you think of a triangle in which the two altitudes of a triangle a...
04:57
|
Playing Now - How many lines of symmetry does the above figure have ? <img src="http...
01:37
|
Play - Which of the following are correct chain isomers of butane ? (i) <img ...
06:07
|
Play - Determine the point of symmetry of a regular hexagon. <img src="htt...
02:11
|
Play - Dtermine the images of the following figure about the given line : ...
01:31
|
Play - Match the following Column A to Column B
02:45
|
Play - Match the following Column A to Column B
02:17
|
Play - Match the following Column A to Column B
05:41
|
Play - Find the area of the figure given below.
02:21
|
Play