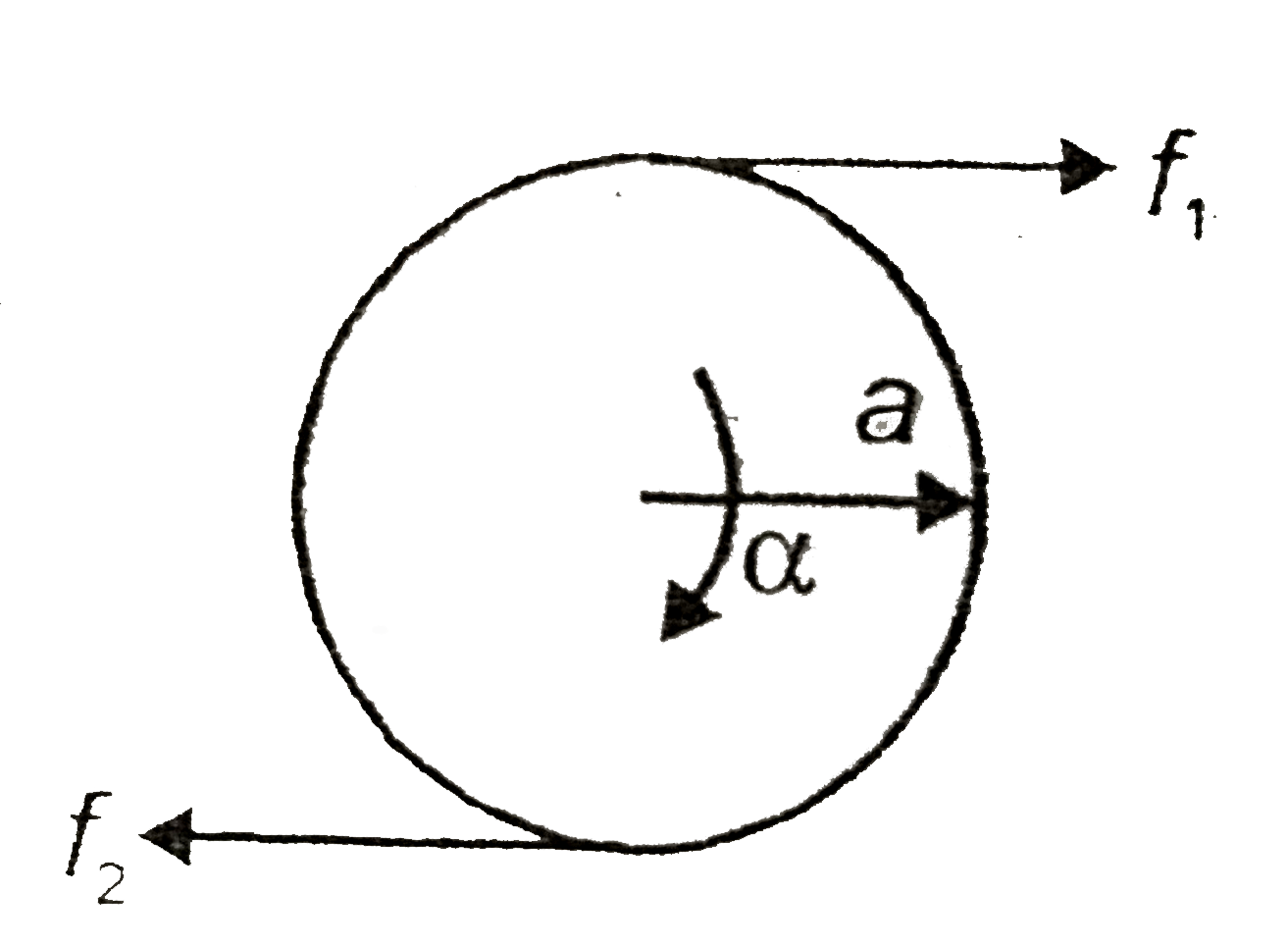
Text Solution
Verified by Experts
|
Topper's Solved these Questions
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
AAKASH INSTITUTE ENGLISH|Exercise Illustration|4 VideosView PlaylistSYSTEM OF PARTICLES AND ROTATIONAL MOTION
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section - A) Objective Type Questions (One option is correct)|62 VideosView PlaylistSEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section-D (Assertion and reason))|5 VideosView PlaylistTEST 1
AAKASH INSTITUTE ENGLISH|Exercise EXERCISE|21 VideosView Playlist
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-SYSTEM OF PARTICLES AND ROTATIONAL MOTION-Try Yourself
- Consider a cylinder of mass M and radius R lying on a rough horizontal...
14:48
|
Playing Now - Two bodies of masses 1kg and 3kg are lying in xy plane at (0,0) and (2...
01:47
|
Play - Three point masses of 1kg, 2kg and 3kg lie at (0,0), (1,2), (3,-1) res...
02:33
|
Play - Three particles of masses m,m and 4kg are kept at a verticals of trian...
03:22
|
Play - Three particles having their masses in the ratio 1 : 3 : 5 are kept at...
02:59
|
Play - Centre of mass of the system lies inside disc or square plate and why ...
02:19
|
Play - Two particles of equal mass are moving along the same line with the sa...
01:09
|
Play - Two particles of equal mass are moving along the same straight line wi...
01:37
|
Play - A shell following a parabolic path explodes somewhere in its flight. T...
01:31
|
Play - All the particles are situated at a distance R from the origin. The di...
03:22
|
Play - Will the velocity and acceleration of centre of mass change if particl...
05:00
|
Play - vecA=(3hati+2hatj-6hatk) and vecB=(hati-2hatj+hatk), find the scalar p...
01:31
|
Play - vecA=(hati-2hatj+6hatk) and vecB=(hati-2hatj+hatk), find the cross pro...
01:10
|
Play - Find a unit vector in the direction of vector vecA=(hati-2hatj+hatk)
01:13
|
Play - Find a vector perpendicular to vector vecA=(hati+2hatj-3hatk) as well ...
02:12
|
Play - The angular displacement of a particle is 24 rad in 10 seconds. Calcul...
01:07
|
Play - The angular velocity of a rigid body is 24 rad s^(-1), Calculate the t...
01:19
|
Play - The angular velocity of circular disc of radius 2cm is 20 rad s^(-1). ...
01:13
|
Play - What is the angular velocity of a particle lying on the axis of rotati...
00:58
|
Play - What is the angular acceleration of a particle moving with constant an...
01:06
|
Play - A wheel is rotating with an angular velocity of 3 rad s^(-1). If the a...
01:30
|
Play