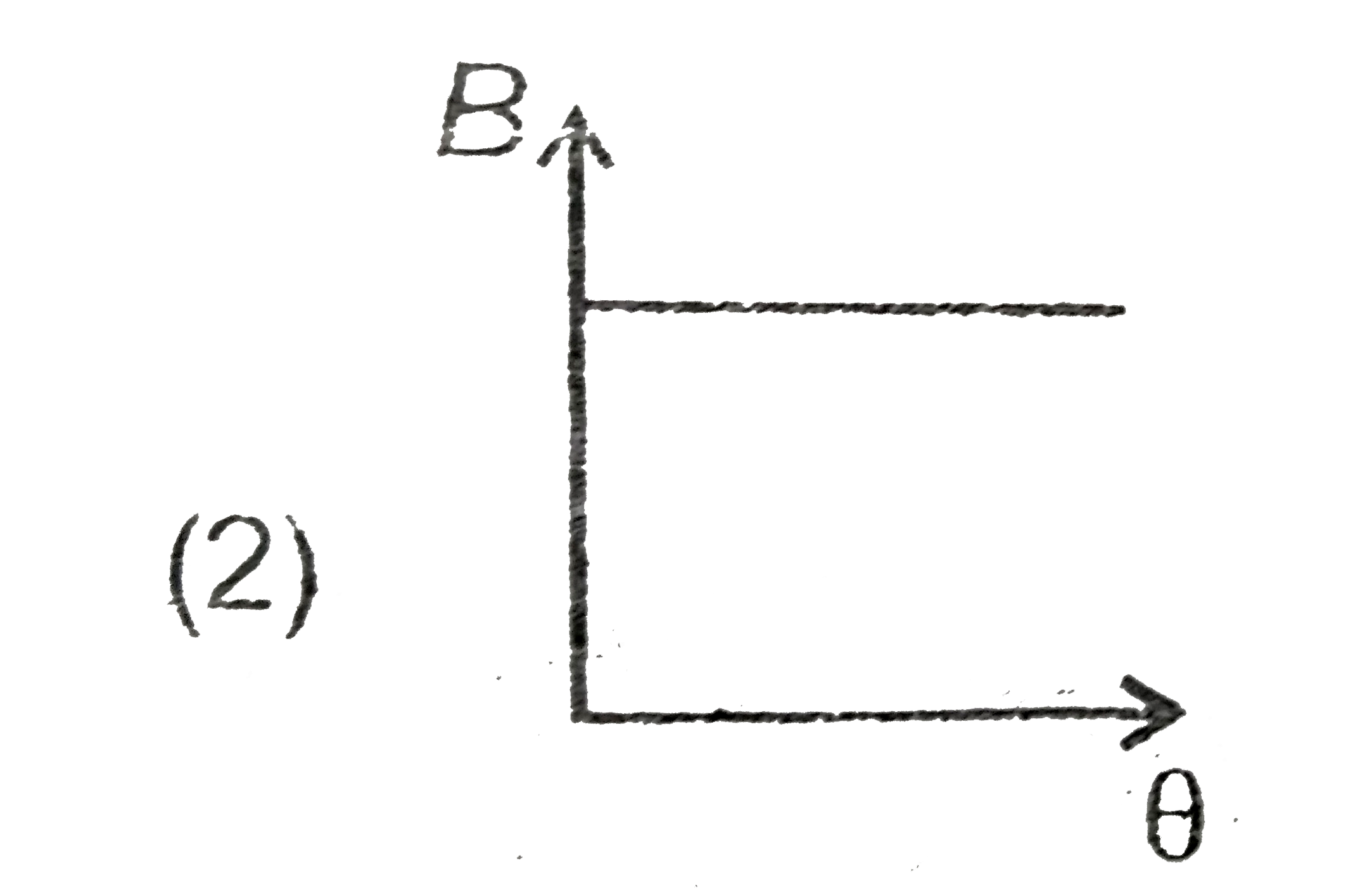
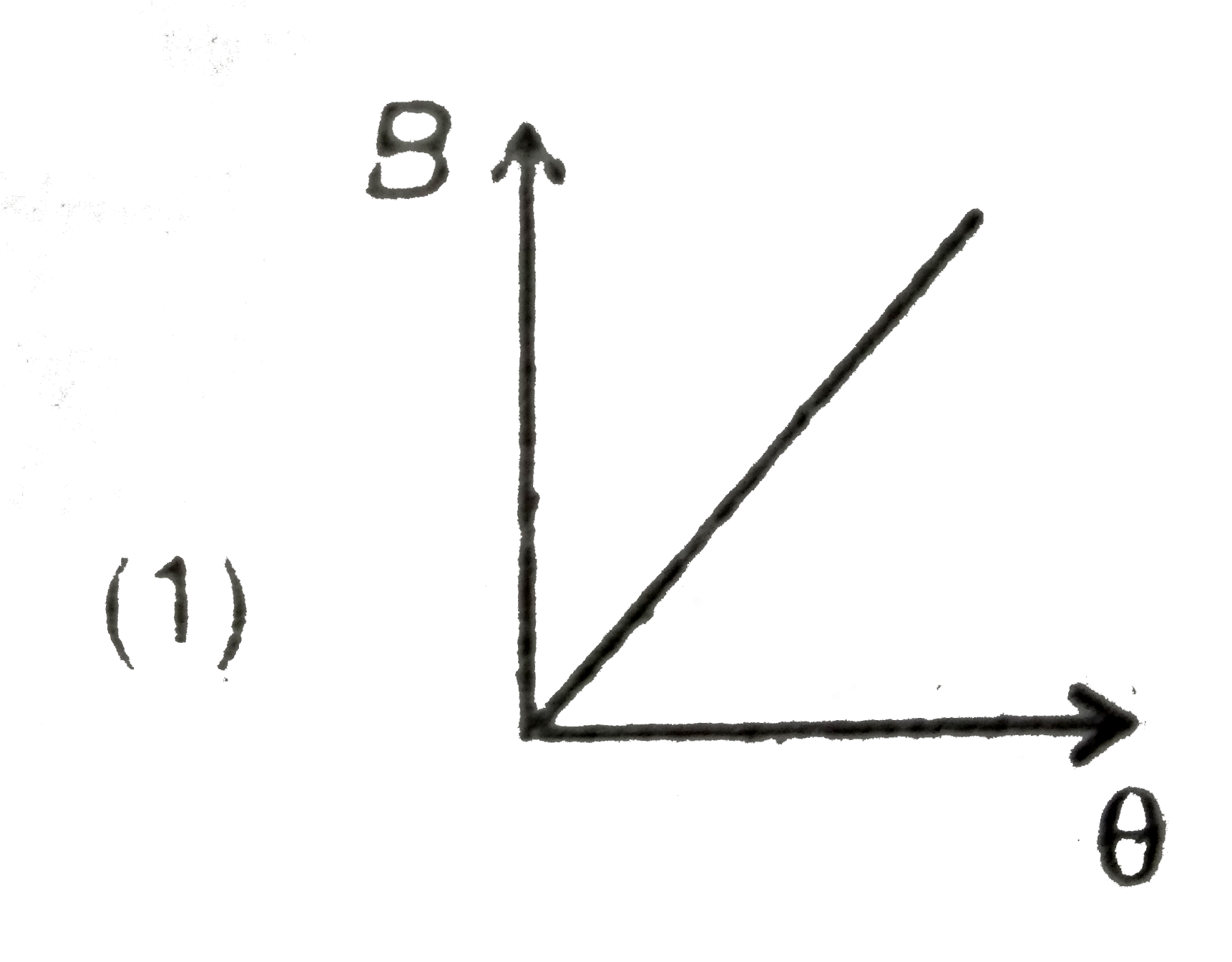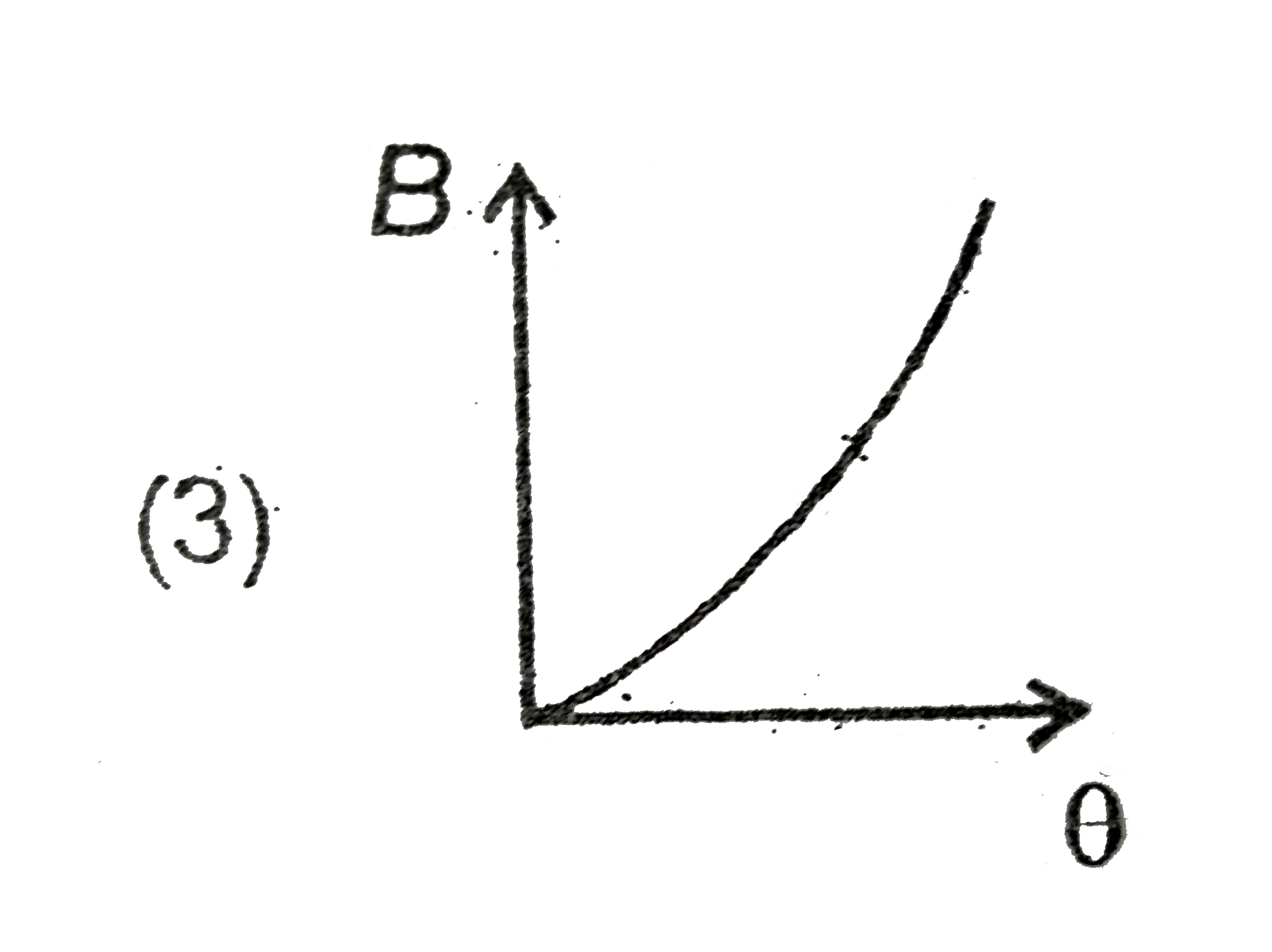A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
MOVING CHARGES AND MAGNETISM
AAKASH INSTITUTE ENGLISH|Exercise Assignment Section C (Objective Type Questions (More than one option are correct)|14 VideosView PlaylistMOVING CHARGES AND MAGNETISM
AAKASH INSTITUTE ENGLISH|Exercise Assignment Section D (Linked Comprehension Type Questions)|10 VideosView PlaylistMOVING CHARGES AND MAGNETISM
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section A) Objective Type Questions (One option is correct)|55 VideosView PlaylistMOVING CHARGE AND MAGNESIUM
AAKASH INSTITUTE ENGLISH|Exercise SECTION D|16 VideosView PlaylistNUCLEI
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT (SECTION-D)|10 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-MOVING CHARGES AND MAGNETISM-Assignment (Section B) Objective Type Questions (One option is correct)
- A wire PQR carrying a current l is bent as shown in the figure. It is ...
02:17
|
Play - In the figure, the current l enters the circular loop of uniform wire ...
04:17
|
Play - An electron is fired parallel to uniform electric and uniform magnetic...
01:40
|
Play - The magnetic field inside a toroidal solenoid of radius R is B. If the...
01:06
|
Play - A square loop of side a carris a current I. The magnetic field at the ...
03:37
|
Play - A proton, a deuteron and an alpha particle moving with equal kinetic ...
03:07
|
Play - A charge q enters into a magnetic field (B) perpendicularly with veloc...
02:11
|
Play - A solid metallic cylinder carriers a direct current. The magnetic fiel...
01:53
|
Play - Two identical magnetic dipoles of magnetic moments 1.0 A-m^(2) each, a...
02:37
|
Play - For a given length l of wire carrying a current l, how many circular t...
02:23
|
Play - Which of the following properties of magnetic line of force differs th...
03:49
|
Play - The earth's magnetic field at a given point is 0.5 xx 10^(-5) Wb m^(-2...
02:04
|
Play - A long thin hollow metallic cylinder of radius R has a current I amper...
02:11
|
Play - A charge q is spread uniformly over an insulated loop of radius r. If ...
01:24
|
Play - If plane of coil and uniform magnetic field B(4T0 is same then torque ...
01:37
|
Play - What is the force experienced by a semicircular wire of radius R when ...
02:02
|
Play - Suppose that a proton travelling in vacuum with velocity V(1) at right...
02:28
|
Play - When two parallel wires carrying current l and 2l in same direction ar...
01:48
|
Play - Calculate the torque acting upon the following structure carrying curr...
02:44
|
Play - Keeping current per unit length of arc constant, the variation of magn...
02:05
|
Playing Now