Home
Class 12
MATHS
In some question of sets, we have to mak...

In some question of sets, we have to make the use of graphs
For example
`A={(x,y):y=e^(x), x in R}`
`B={{x,y}: y=-x. x in R}`
Find `n(A cap B)`

It is clear that `y=e^(x) and y=-x` intersect at one pont. Hence `n(A cap B)=1`
`A:{(x,y):y=sqrt(4-x^(2)), x in [-2,2]}`
`B={(x,y):y=|x|, x in R}`
Then `n(A cap B)`

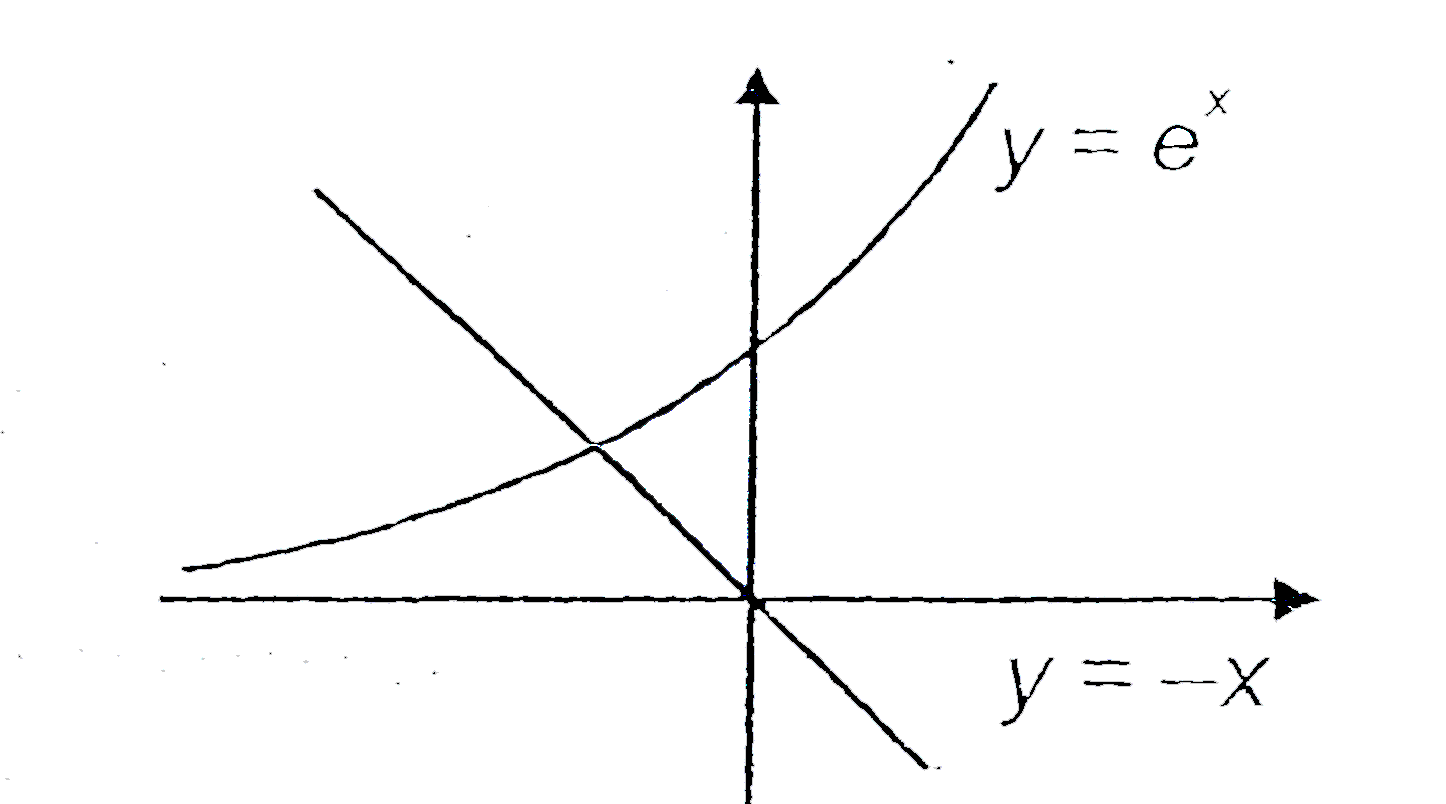
Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • SETS

    AAKASH INSTITUTE ENGLISH|Exercise COMPREHENSION-III|3 Videos

  • SETS

    AAKASH INSTITUTE ENGLISH|Exercise SECTION-E(Assertion-Reason Type Questions)|2 Videos

  • SETS

    AAKASH INSTITUTE ENGLISH|Exercise SECTION-D(Linked Comprehension Type Questions))|3 Videos

  • SEQUENCES AND SERIES

    AAKASH INSTITUTE ENGLISH|Exercise Assignment (SECTION - J) Aakash Challengers|11 Videos

  • STATISTICS

    AAKASH INSTITUTE ENGLISH|Exercise Section-C Assertion-Reason|15 Videos

Similar Questions

Explore conceptually related problems

In some question of sets, we have to make the use of graphs For example A={(x,y):y=e^(x), x in R} B={{x,y}: y=-x. x in R} Find n(A cap B) It is clear that y=e^(x) and y=-x intersect at one pont. Hence n(A cap B)=1 A={(x,y):x^(2)+y^(2) le 2, x ,y in R} B={{x,y): y gex^(2),x,y in R} Then domain of A cap B is

In some question of sets, we have to make the use of graphs For example A={(x,y):y=e^(x), x in R} B={{x,y}: y=-x. x in R} Find n(A cap B) It is clear that y=e^(x) and y=-x intersect at one pont. Hence n(A cap B)=1 A={(x,y):y = sin pi x,x in R} B={(x,y):y=|In|x"||",x in R-{0}} Then, n(A cap B)

if A={(x,y):x^(2)+y^(2)=4, x,y in R }and B={(x,y):Y=|x|, x , y in R } then

If the sets A and B are defined are defined as A={(x,y):y=e^x, x in R},B={(x,y):y=x, x in R} then

If A={(x,y}: y=3^(x), y in R} and B={{x,y}:y=x, x,y in R} then which of the following is true?

If A={(x ,\ y): y=e^x ,\ x in R}a n d\ B={(x , y): y=e^(-x),\ x in R} , then write AnnBdot

If set A and B are defined as A = {(x,y)|y = 1/x, 0 ne x in R}, B = {(x,y)|y = -x , x in R,} . Then

If A={(x ,\ y): y=1/x ,\ 0!=x in R}a n d\ B={(x , y): y=-x ,\ x in R} , then write AnnBdot

if A={(x,y):x^(2)+y^(2)=4,x,y in R } and B={(x,y): x^(2)+y^(2)= 9,x,yin R} ,then

if A={(x,y):y=(4)/(x),xne0}and B= {(x,y):x^(2)+y^(2)=8,x,yin R} ,then