Statement : "Energy can be neither created nor destroyed but it can be converted from one form to another form . (or) The total energy of a closed system always remains constant" is called law of conservation of energy .
Poof : In the case of a body projected vertically upwards :
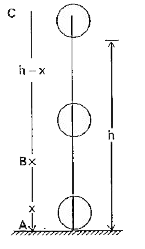
Suppose a body of mass .m. is projected vertically upwards with an initial velocity .u. from the ground at .A. as shown in figure
The total mechanical energy (E) = KE + PE
Let A, B, C be the points on the ground, at heights .h. and .H. respectively
At .A.: P.E of the body`= mg xx 0 = 0 ` [`:. h = 0 `]
Kinetic energy `K.E = (1)/(2) m u^(2)`
Total mechanical energy `(E_(A)) at .A. = PE +KE = 0 + (1)/(2) m u^(2)`
`E_(A) = (1)/(2)m u^(2)` . . . . (1)
At .B. : When the body reaches the point .B. at a height .h. . Velocity of the body `V_(B) at ` .B. can be determined using the equation
`{:(v^(2) - u^(2) = 2as," Here "),(v_(B)^(2) - u^(2) = 2 (-g)h," " u = u ),(v_(B)^(2) = u^(2) - 2gh," "v = v_(B) = ? a = g"," s = h ):}`
`KE =(1)/(2) mv_(B)^(2) = (1)/(2) m (u^(2) - 2gh) = (1)/(2) m u^(2) - mgh`
Potential energy (P.E) = mgh
Total mechanical energy `(E_(B)) at B = P.E + K.E`
`E_(B) = mgh + (1)/(2) m u^(2) - mgh`
`E_(B) = (1)/(2) m u^(2) . . . . (2)`
At C : When the body reaches the maximum height (H) above the ground ,its final velocity becomes zero. Maximum height `(H) = (u^(2))/(2g)`
P.E. of the body = mgH = mg `((u^(2))/(2g))`
P.E `= (1)/(2) m u^(2)`
K.E. of the body = 0
Total mechanical energy at .C. `(E_(c)) = (1)/(2) m u^(2) + 0 `
`E_(c) = (1)/(2) m u^(2) . . . (3)`
From the above three equations the total mechanical energy of the system remains constant. Hence law of conservation of energy is proved in case of vertically projected body