Topper's Solved these Questions
CHAPTERWISE REVISION (STAGE 3)
ICSE|Exercise CIRCLE|7 VideosCHAPTERWISE REVISION (STAGE 3)
ICSE|Exercise STATISTICS|5 VideosCHAPTERWISE REVISION (STAGE 3)
ICSE|Exercise CONSTRUCTIONS OF POLYGONS |4 VideosCHAPTERWISE REVISION (STAGE 1)
ICSE|Exercise Graphical solution |10 VideosCIRCLE
ICSE|Exercise EXERCISE 17(D)|12 Videos
Similar Questions
Explore conceptually related problems
ICSE-CHAPTERWISE REVISION (STAGE 3) -AREA
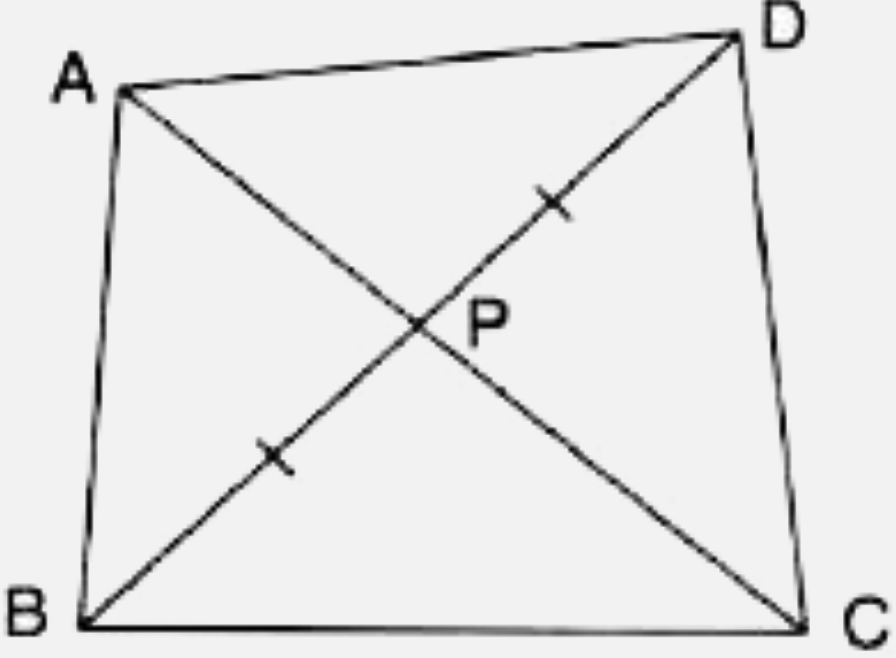
- In quadrilateral ABCD, diagonal BD is bisected by the diagonal AC. Pro...
Text Solution
|
- In Delta ABC, E is mid-point of side AB and EBCD is a parallelogram. I...
Text Solution
|
- In the following figure, F and E are points on the side AD of the tria...
Text Solution
|
- Any point D is taken on the side BC of a Delta ABC and AD is produce...
Text Solution
|
- ABC is an equilateral triangle. Taking BC as the base, construct a rig...
Text Solution
|