Home
Class 10
MATHS
Two circles touch each other externally ...

Two circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.

Answer

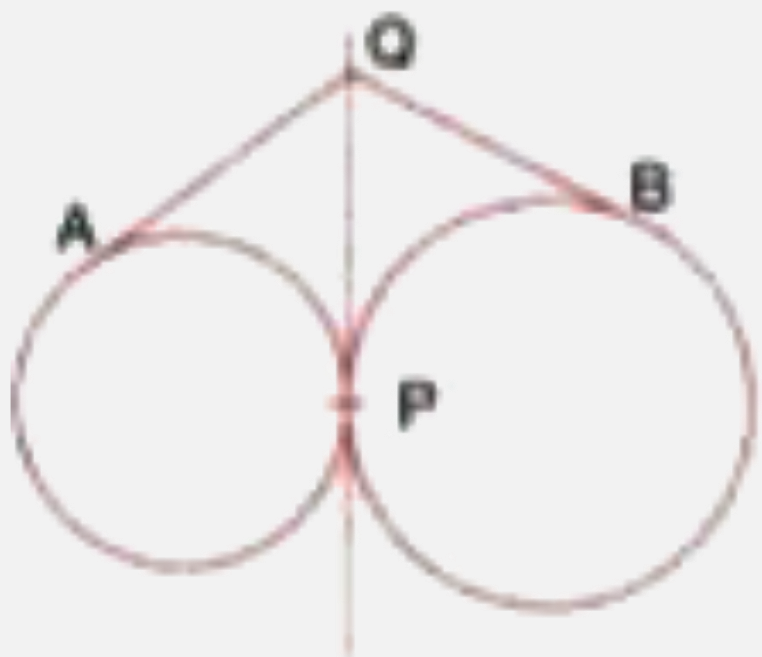
Step by step text solution for Two circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal. by MATHS experts to help you in doubts & scoring excellent marks in Class 10 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • TANGENTS AND INTERSECTING CHORDS

    ICSE|Exercise EXERCISE 18 (B)|18 Videos

  • TANGENTS AND INTERSECTING CHORDS

    ICSE|Exercise EXERCISE 18 (C)|42 Videos

  • TANGENTS AND INTERSECTING CHORDS

    ICSE|Exercise EXERCISE 18 (C)|42 Videos

  • SPECIMEN QUESTION PAPER (MATHEMATICS)

    ICSE|Exercise Section C|12 Videos

  • TRIGONOMETRICAL IDENTITIES

    ICSE|Exercise QUESTIONS|22 Videos

Similar Questions

Explore conceptually related problems

In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that: (i) tangent at point P bisects AB (ii) angle APB=90^(@)

Two circles touch each other externally at P . A B is a common tangent to the circle touching them at A and B . The value of /_A P B is (a) 30^o (b) 45^o (c) 60^o (d) 90^o

Knowledge Check

  • Two circles with radii 25 cm and 9 cm touch each other externally. Find the length of the direct common tangent.

    A
    32 cm
    B
    50 cm
    C
    40 cm
    D
    30 cm

    • Similar Questions

    Explore conceptually related problems

    In Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .

    In the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.

    Two circles touch externally at a point P . From a external point T on the tangent at P , tangents T Q and T R are drawn to the circles with points of contact Q and R respectively. Prove that T Q = T R .

    Two circles touch each other internally at point P. QPR is the tangent at P, segments PAB and PCD meet circles at points, A,B,C and D as shown in the figure. Show that chord AC is parallel to chord BD.

    Two circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent, are equal in length.

    Two circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.

    Two equal circles touch each other externally at C and A B is a common tangent to the circles. Then, /_A C B= 60o (b) 45o (c) 30o (d) 90o

    Home
    Profile