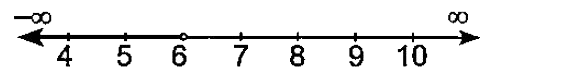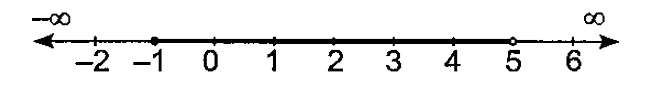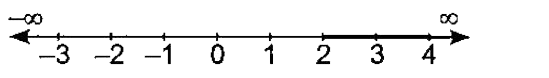Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
REVISION PAPER -4
ICSE|Exercise SECTION - B|26 VideosView PlaylistREVISION PAPER -3
ICSE|Exercise SECTION - B|22 VideosView PlaylistREVISION PAPER -5
ICSE|Exercise SECTION B|28 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
ICSE-REVISION PAPER -4-SECTION - B
- Find the range of vaues of x, which satisfy the inequality : -1/5 l...
04:54
|
Playing Now - In the given I is the incentre of triangle ABC. AI produced meets the ...
02:46
|
Play - The equal chords AB and CD of circle with centre O, when produced, mee...
02:55
|
Play - The equal chords AB and CD of circle with centre O, when produced, mee...
05:17
|
Play - A man wants to buy 124 shares available at rupes 66 (par value = rupe...
04:56
|
Play - A man wants to buy 124 shares available at rupes 66 (par value = rupe...
04:56
|
Play - A man wants to buy 124 shares available at rupes 66 (par value = rupe...
04:56
|
Play - Two circles touch each other extermally at point P. APC and BPD are st...
04:30
|
Play - Two circles touch each other extermally at point P. APC and BPD are st...
04:22
|
Play - 21 glass spheres, each of radius 2cm are packed in a cuboidal box of ...
03:44
|
Play - The point P divides the joining of (2,1) and (-3,6) in the ratio 2:3. ...
03:51
|
Play - Find the common ratio of an infinte GP. Whose each term is ten times t...
04:22
|
Play - A dividend of 9% was declared on 100rs share selling at a certain pric...
02:52
|
Play - A divident of 9% was declear on Rs 100 shares selling at a certain pri...
02:48
|
Play - A circle, with centre O, circumscribs a pentagon ABCDE. IF AB- BC= CD ...
03:59
|
Play - A circle, with centre O, circumscribs a pentagon ABCDE. IF AB- BC= CD ...
03:58
|
Play - A circle, with centre O, circumscribs a pentagon ABCDE. IF AB- BC= CD ...
03:38
|
Play - The hotel bill for a number of persons for overnight stay is Rs 4,800 ...
06:03
|
Play - Show that any four vertices of a regular pentagon form a cyclic quadri...
04:47
|
Play - If cos ec theta - sin theta = m and sec theta - cos theta = n, then sh...
04:28
|
Play - about to only mathematics
03:58
|
Play