Home
Class 11
PHYSICS
Three identical rods of length 1 m each,...


Three identical rods of length 1 m each, having cross-sectional area of `1cm^2` each and made of aluminium, copper and steel, respectively, are maintained at temperatures of `12^@C`,`4^@C` and `50^@C`, respectively, at their separate ends. Find the teperature of their common junction.
`[K_(Cu)=400 W//m-K,K_(Al)=200 W//m-K,K_("steel")=50 W//m-K]`

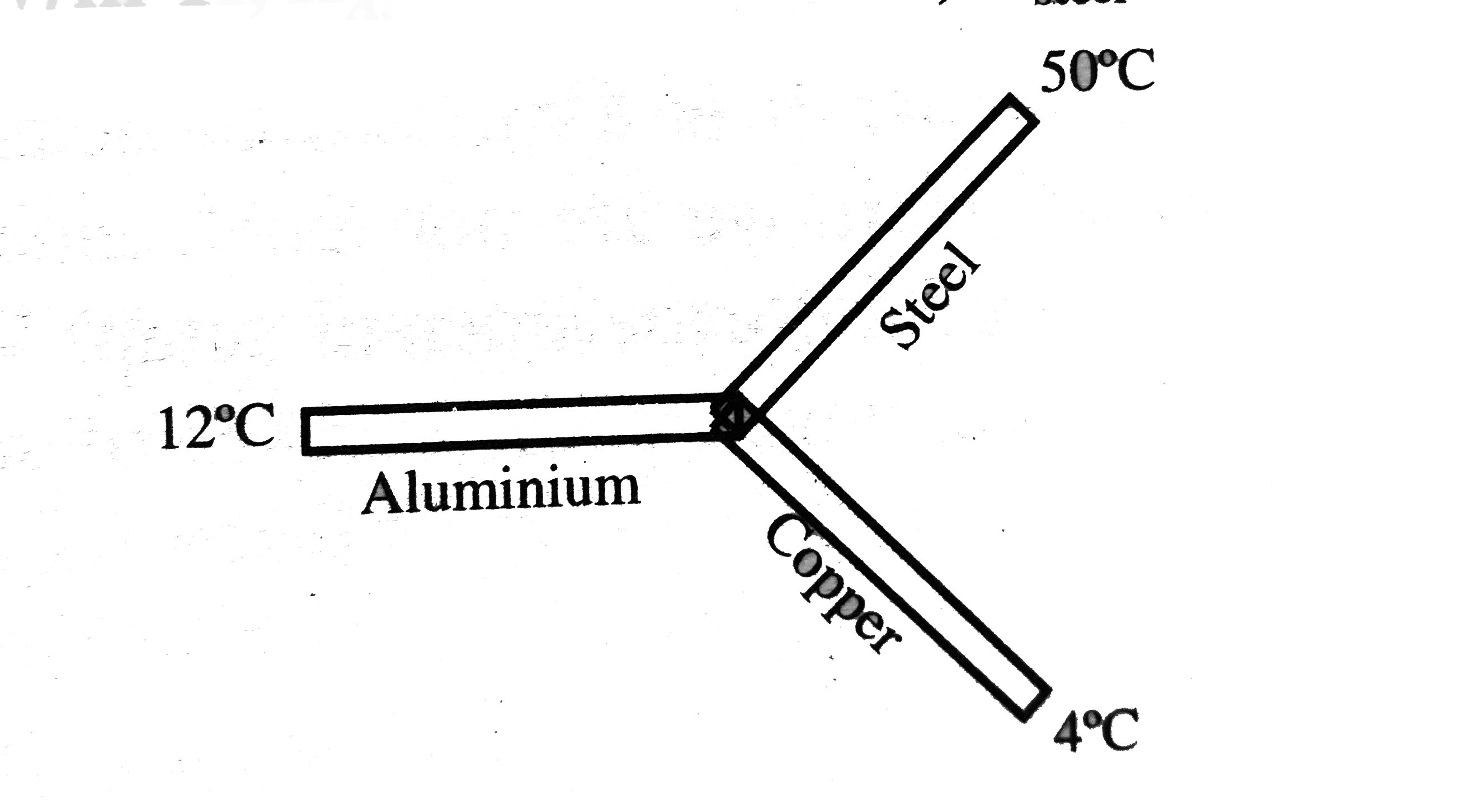
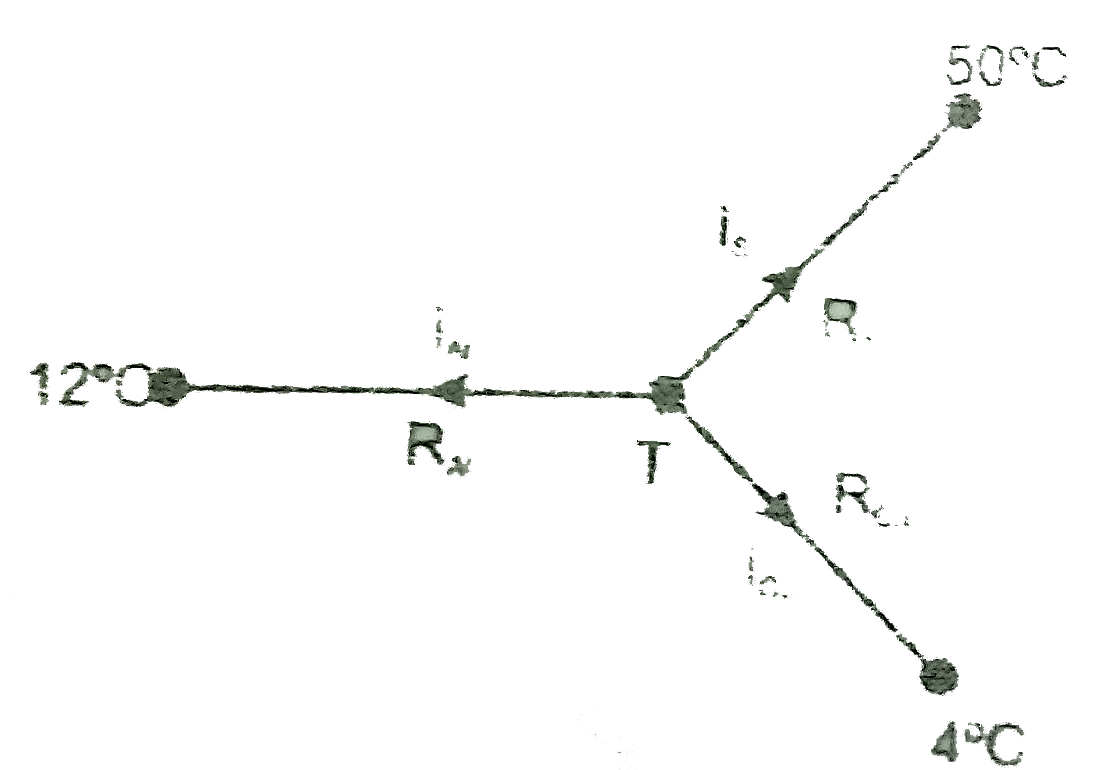
Text Solution

Verified by Experts

`R_(AI) = (L)/(KA) = (1)/(10^(-4)xx200) = (10^(4))/(200)`
Similarly `R_(stell) = (10^(4))/(50)` and `R_(copper) = (10^(4))/(400)`
Let temperature of common junction `= T` then from Kirchoff's current laws,
`i_(AI) +i_(steel) +i_(Cu) = 0`
`rArr (T-12)/(R_(AI)) +(T-50)/(R_(steel)) +(T-4)/(R_(Cu)) = 0`
`rArr (T-12) 200 +(T - 50) 50 +(T-4) 400`
`rArr 4(T-12) +(T-50) +8(T-4) = 0`
`rArr 13T = 48 +50 +32 = 130`
`rArr T = 10^(@)C`
Promotional Banner

Topper's Solved these Questions

  • HEAT TRANSFER

    RESONANCE ENGLISH|Exercise Board Level Exercise|14 Videos

  • HEAT TRANSFER

    RESONANCE ENGLISH|Exercise Exercise-1|1 Videos

  • HEAT TRANSFER

    RESONANCE ENGLISH|Exercise Advancel Level Problems|17 Videos

  • GRAVITATION

    RESONANCE ENGLISH|Exercise Exercise|21 Videos

  • KINEMATICS

    RESONANCE ENGLISH|Exercise Exercise|65 Videos

Similar Questions

Explore conceptually related problems

Three copper rods and three steel rods each of length l = 10 cm and area of cross-section 1cm^(2) are connected as shown If ends A and E are maintained at temperatures 125^(@)C and 0^(@)C respectively, calculate the amount of heat flowing per second from the hot of cold function. [K_(Cu) = 400 W//m-K, K_(steel) = 50 W//m-K]

Four identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T_(1) , T_(2) and T_(3) respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.

Four identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T_(1) , T_(2) and T_(3) respectively. Assuming no loss of heat to the atmosphere, find the temperature at B .

A body of length 1 m having cross sectional area 0.75 m^(2) has heat flow through it at the rate of 6000 "Joule"//sec . Then find the temperature difference if K = 200 Jm^(-1) K^(-1) .

A copper rod of length 75 cm and an iron rod of length 125cm are joined together end to end . Both are of circular cross section with diameter 2 cm . The free ends of the copper and iron are maintained at 100^@C and 0^@C respectively . The surface of the bars are insulated thermally . The temperature of the copper -iron junction is [Thermal conductivity of the copper is 386.4 W//m-K and that of iron is 48.46W//m-K ].

All the rods have same conductance 'K' and same area of cross section ' A' . If ends A and C are maintained at temperature 2T_(0) and T_(0) respectively then which of the following is // are correct?

A bar of copper of length 75cm and a bar of steel of length 125cm are joined together end to end. Both are of circular cross section with diameter 2cm . The free ends of the copper and the steel bars are maintained at 100^(@)C and 0^(@)C respectively. The curved surface of the bars are thermally insulated. What is the temperature of the copper-steel junction? What is the amount of heat transmitted per unit time across the junction? Thermal conductivity of copper is 386Js^(-1)m^(-1) C^(-1) and that of steel is 46Js^(-1)m^(-1) C^(-1)

Three rods of the same dimensions have thermal conductivities 3 k , 2 k and k . They are arranged as shown, with their ends at 100^(@)C, 50^(@)C and 0^(@)C . The temperature of their junction is :-

Two bars of thermal conductivities K and 3K and lengths 1 cm and 2 cm respectively have equal cross-sectional area, they are joined lengths wise as shown in the figure. If the temperature at the ends of this composite br is 0^(@)C and 100^(@)C respectively (see figure), then the temperature phi of the interface is

The ends of a copper rod of length 1m and area of cross-section 1cm^2 are maintained at 0^@C and 100^@C . At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400 Wm^-1 K^-1 .