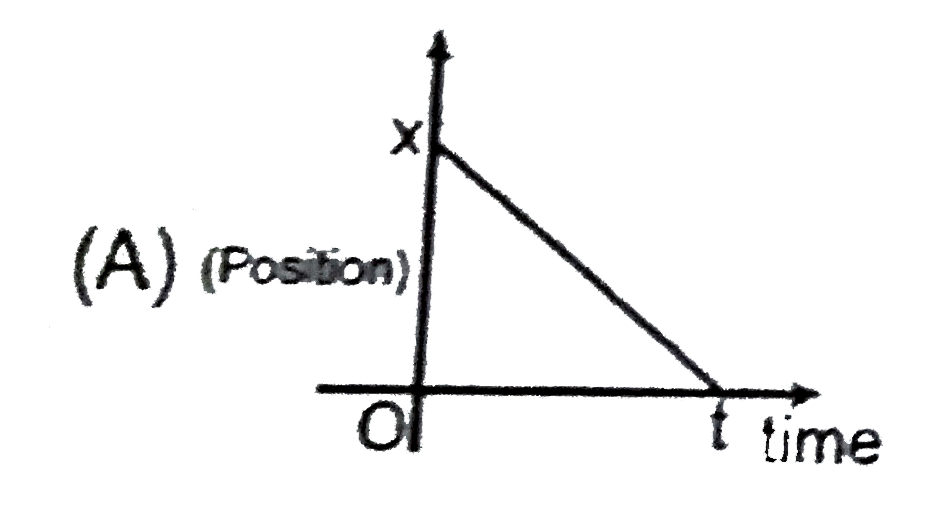
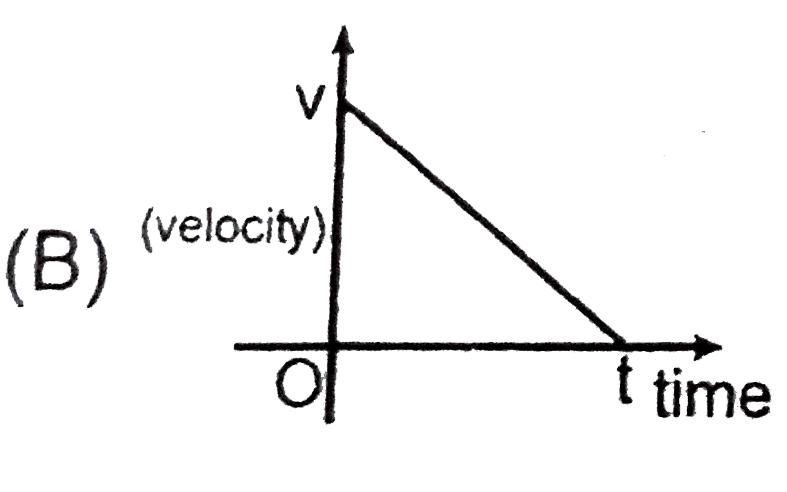
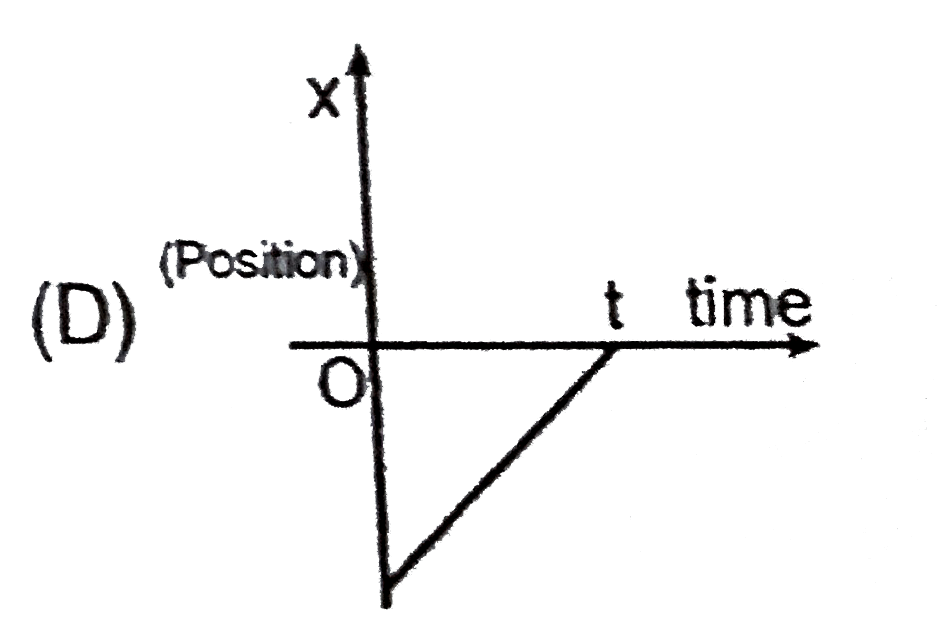
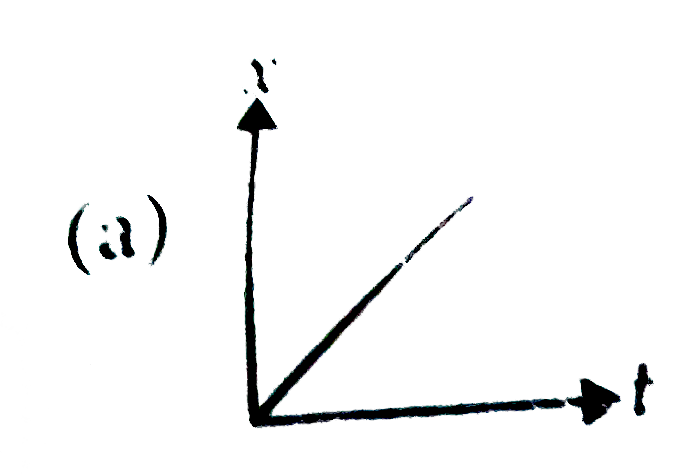
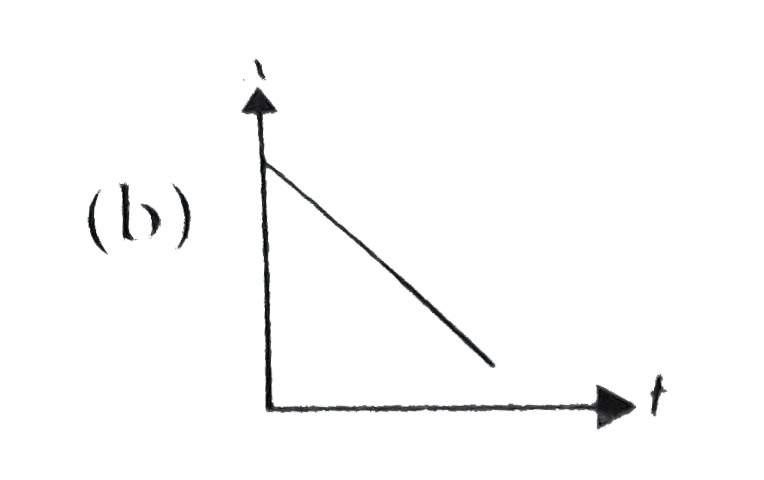
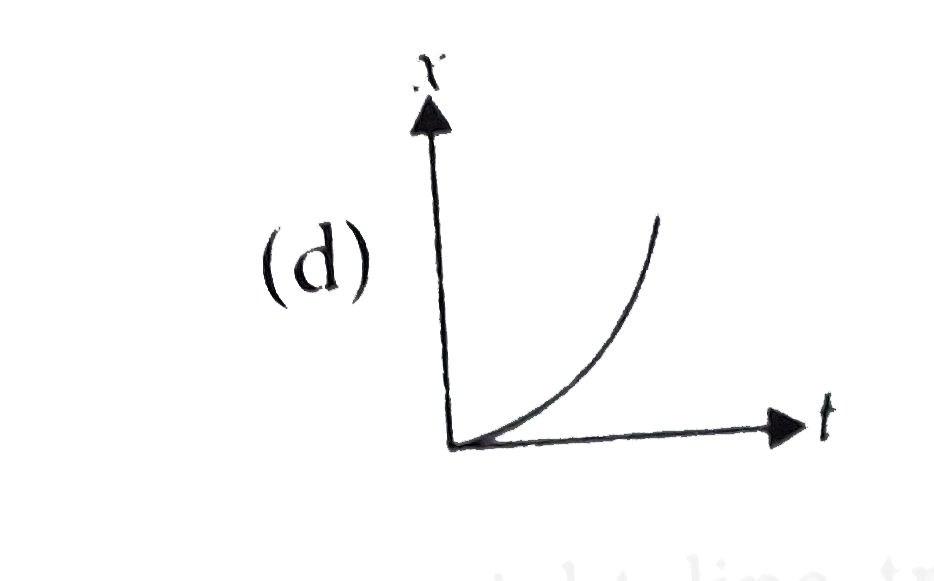A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 20|8 VideosView PlaylistDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 21|8 VideosView PlaylistDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 18|7 VideosView PlaylistCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise Exercise|53 VideosView PlaylistELASTICITY AND VISCOCITY
RESONANCE ENGLISH|Exercise Advanced Level Problems|9 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEMS-dpp 19
- For which of the following graphs the average velocity of a particl mo...
05:41
|
Playing Now - Variation of displacement x of a particle moving on a straight line wi...
04:53
|
Play - A particle is projected at an angle 60^@ with speed 10(sqrt3)m//s, fro...
Text Solution
|
Play - Two cars A and B are racing along straight line. Car A is leading, suc...
05:44
|
Play