A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 49|6 VideosView PlaylistDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise DPP 50|5 VideosView PlaylistDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 47|7 VideosView PlaylistCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise Exercise|53 VideosView PlaylistELASTICITY AND VISCOCITY
RESONANCE ENGLISH|Exercise Advanced Level Problems|9 VideosView Playlist
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEMS-dpp 48
- A disc (of radius r cm) of uniform thickness and uniform density sigma...
04:29
|
Playing Now - A flywheel rotates with a uniform angular acceleration. Its angular ve...
03:19
|
Play - Figure shows the roller coaster track. Each car will start from rest a...
06:43
|
Play - A crate of mass m is pulled with a force F along a fixed right angles ...
03:33
|
Play
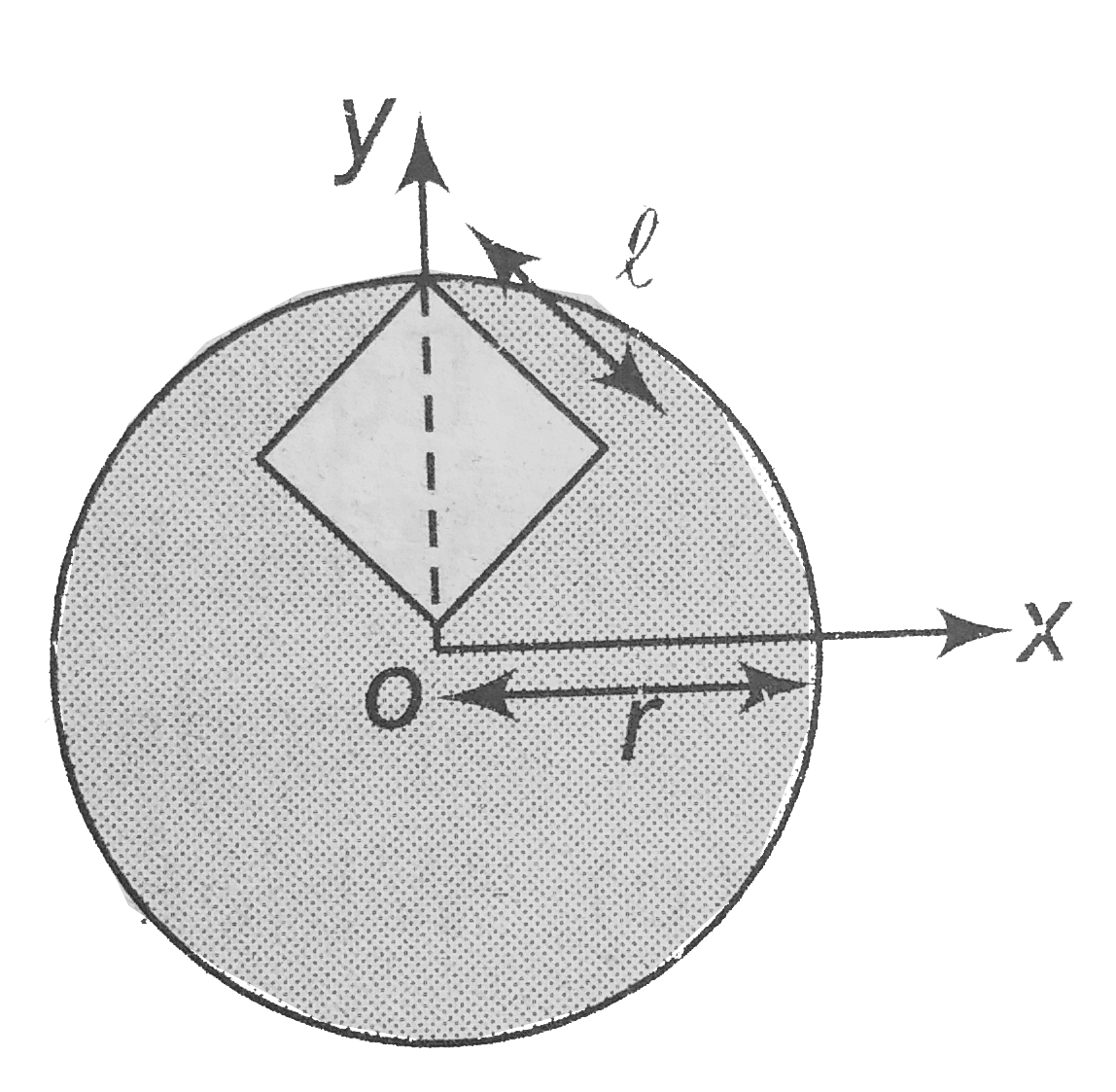 .
.