Home
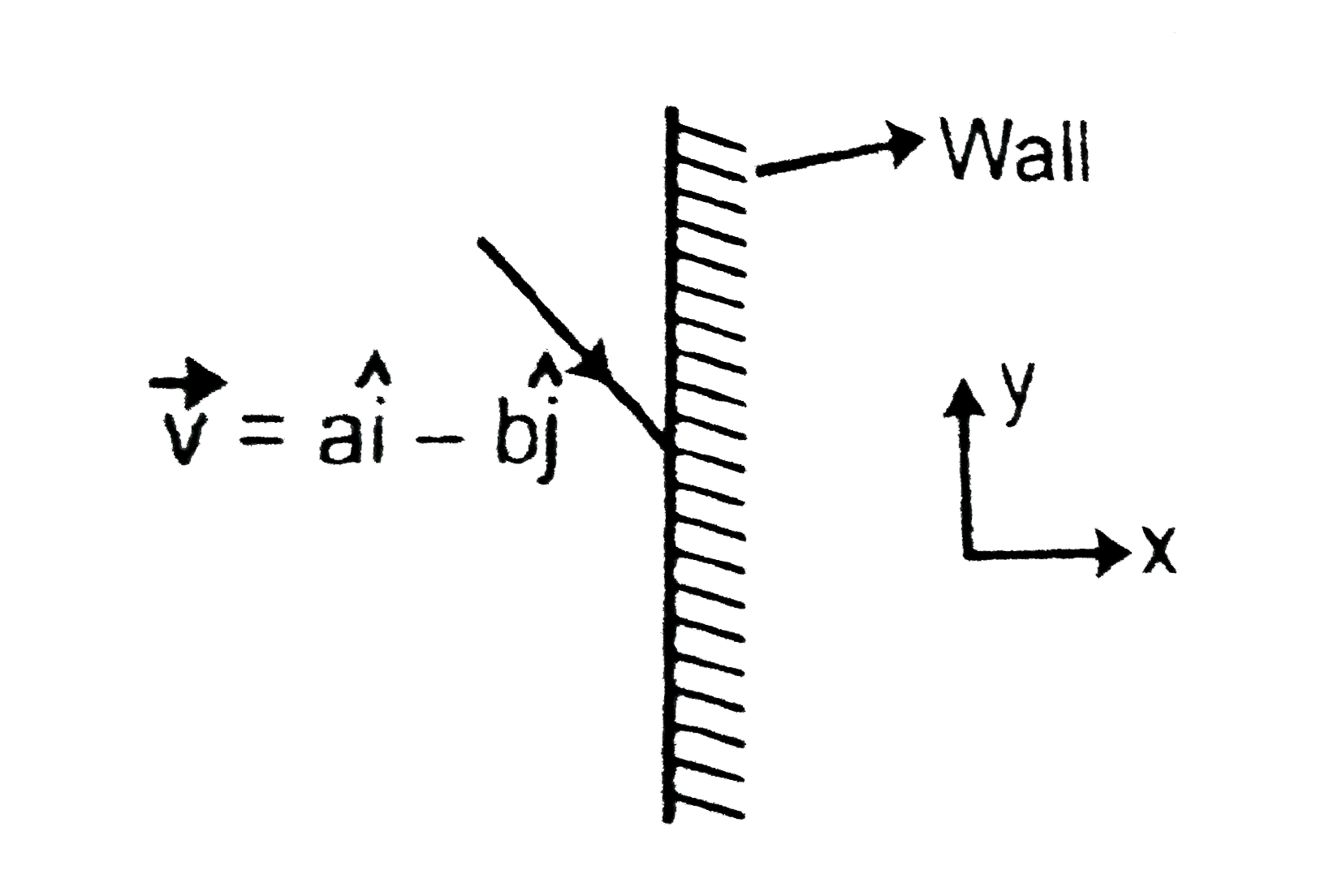
Class 11
PHYSICS
A glass ball collides with a smooth hori...

A glass ball collides with a smooth horizontal surface (`xz` plane) with a velocity `V = ai- bj`. If the coefficient of restitution of collision be `e`, the velocity of the ball just after the collision will be

A

`hat(i)+b hat(j)`

B

`ahat(i)+e b hat(j)`

C

`a hat(i)-b hat(j)`

D

`ahat(i)-e b hat(j)`

Text Solution

Verified by Experts

The correct Answer is:
B
A collision which is not elastic changes only the normal component of velocity .
Here the normal component is `-b`. Hence it become `(+eb)`
after collision keeping the `x-` component (tangential)
as begore collision.
`rArr vec(v)_(f)=ahat(i)+ebhat(j)`

Hence `(B)`.
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 56|7 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 57|7 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 54|8 Videos

  • CURRENT ELECTRICITY

    RESONANCE ENGLISH|Exercise Exercise|53 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

A glass ball collides with an identical ball at rest with v_(0)=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.

A ball collides with a frictionless wall with velocity u as shown in the figure. Coefficient of restitution for the impact is e. (a) Find expression for the velocity of the ball immediately after the impact. (b) If impact is perfectly elastic what do you observe?

Knowledge Check

  • A ball of mass m moving with a speed 2v_0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?

    A
    `(1-e)/(1+e)`
    B
    `(1+e)/(1-e)`
    C
    `(e-1)/(e+1)`
    D
    `(e+1)/(e-1)`

  • A ball of mass m moving with a speed 2v_0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?

    A
    `(1-e)/(1+e)`
    B
    `(e-1)/(e+1)`
    C
    `(1+e)/(1-e)`
    D
    `(e+1)/(e-1)`

    • Similar Questions

    Explore conceptually related problems

    A ball moving with speed v collides with a horizontal smooth surface at an angle theta with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'

    A ball P is moving with a certain velocity v , collides head-on with another ball Q of same mass at rest. The coefficient of restitution is 1/4, then ratio of velocity of P and Q just after the collision is

    A small ball of mass m collides with as rough wal having coeficient of friction mu at an angle theta with the normal to the wall. If after collision the ball moves wilth angle alpha with the normal to the wall and the coefficient of restitution is e , then find the reflected velocity v of the ball just after collision.

    A ball collides elastically with a massive wall moving towards it with a velocity of v as shown. The collision occurs at a height of h above ground level and the velocity of the ball just before collision is 2v in horizontal direction. The distance between the foot of the wall and the point on the ground where the ball lands, at the instant the ball lands, will be :

    The first ball of mass m moving with the velocity upsilon collides head on with the second ball of mass m at rest. If the coefficient of restitution is e , then the ratio of the velocities of the first and the second ball after the collision is

    A ball moving with velocity 2 ms^(-1) collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5 , then their velocities (in ms^(-1) ) after collision will be

    Home
    Profile