Recommended Questions
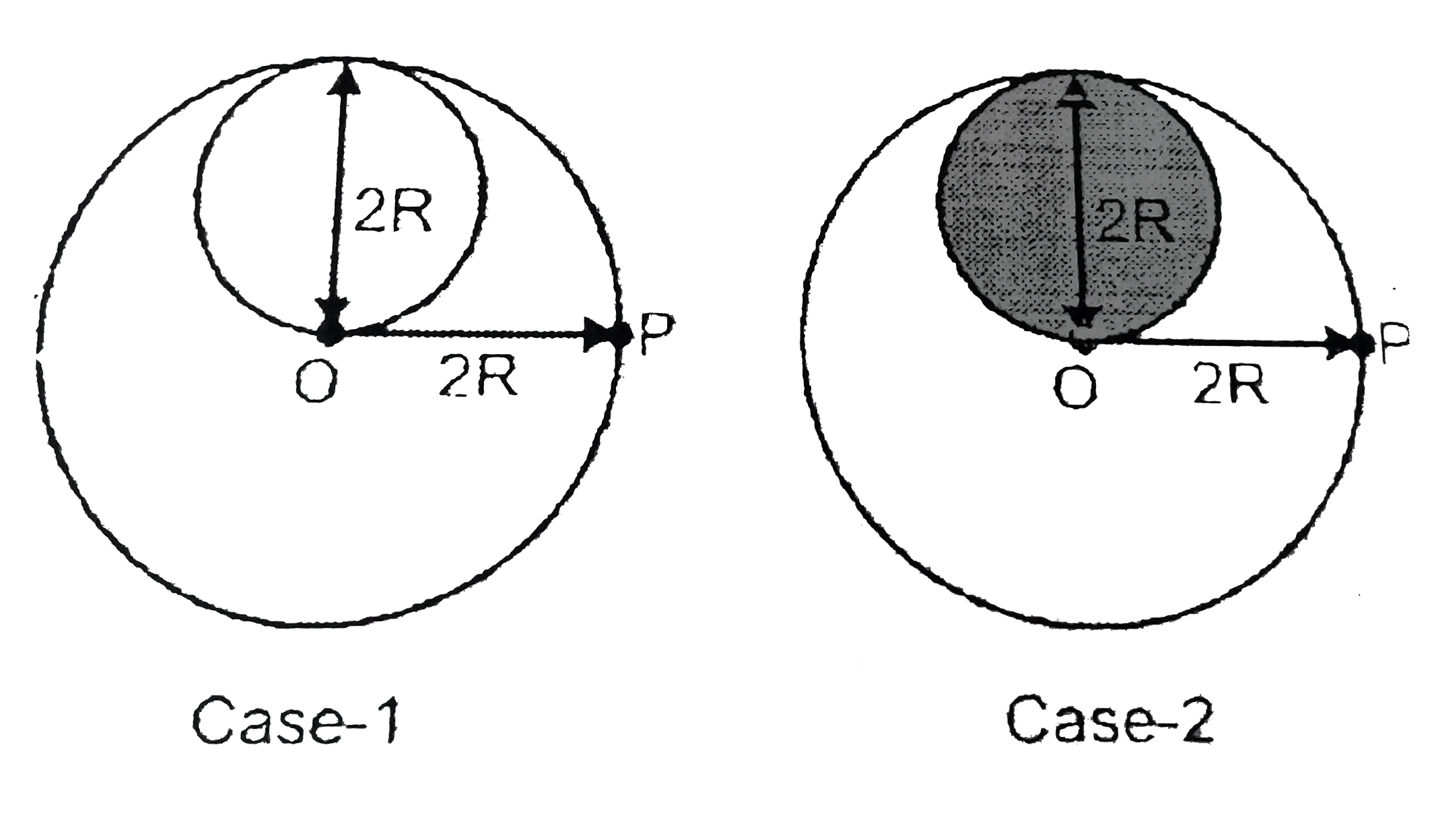
- A lamina is made by removing a small disc of diameter 2 R from a bigge...
05:34
|
Playing Now - A lamina is made by removing a small disc of diameter 2R from a bigg...
03:57
|
Play - A circular disc of radius R is removed from a bigger circular disc of ...
01:47
|
Play - A small hole is made in a disc of mass M and radius R at a distance R/...
01:23
|
Play - A lamina is made by removing a small disc of diameter 2 R from a bigge...
08:38
|
Play - On the flat surface of a disc of radius a a small circular hole of rad...
02:53
|
Play - A circular disc of radius R is removed from a bigger circular disc of ...
03:41
|
Play - A circular disc of radius R is removed from a bigger circular disc of ...
03:43
|
Play - A circular disc of radius R is removed from a bigger circular disc of ...
03:43
|
Play