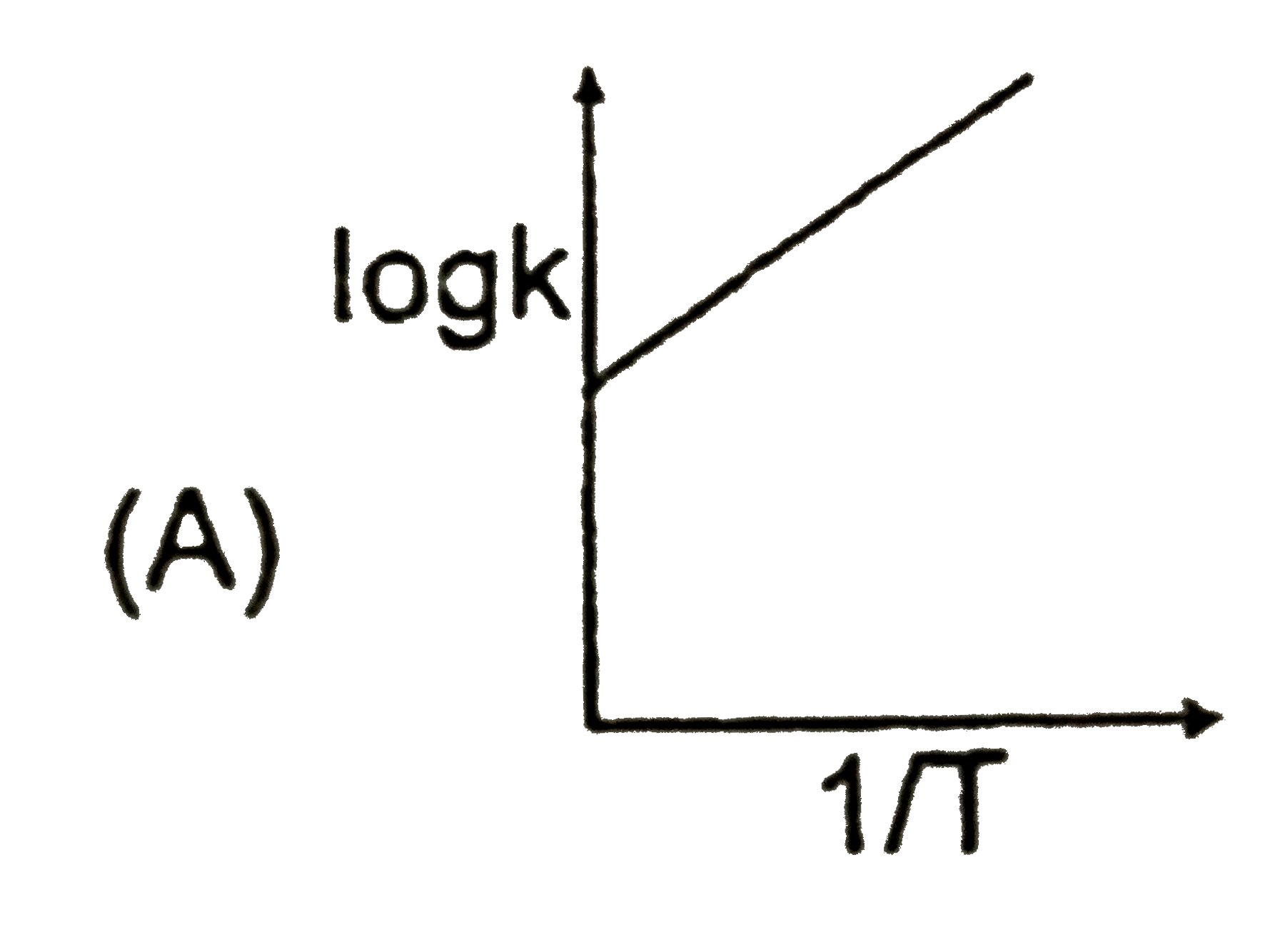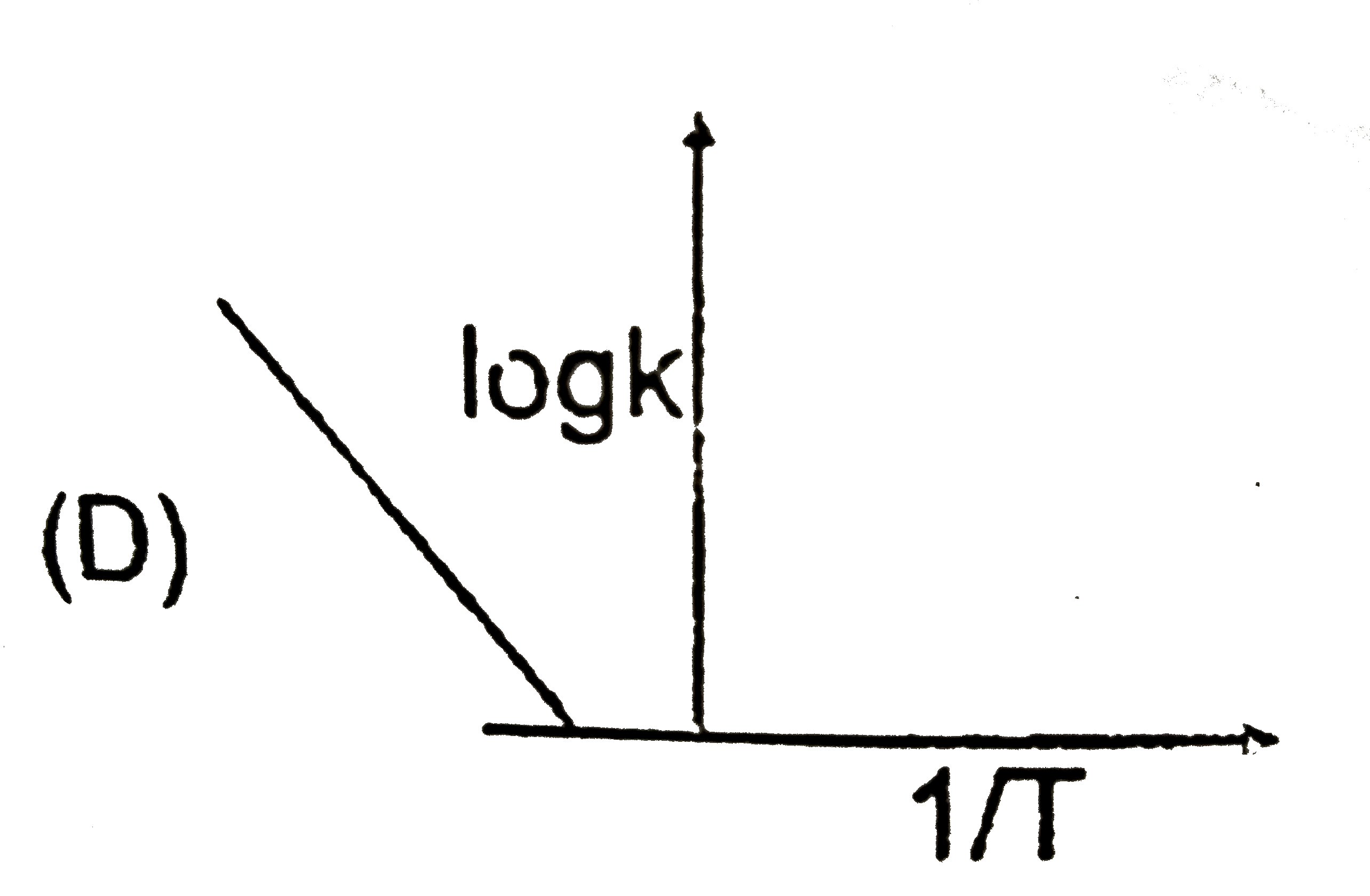A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
CHEMICAL EQUILIBRIUM
RESONANCE ENGLISH|Exercise Exercise-3 (Part-1)|6 VideosView PlaylistCHEMICAL EQUILIBRIUM
RESONANCE ENGLISH|Exercise Exercise-3 (Part-2)|17 VideosView PlaylistCHEMICAL EQUILIBRIUM
RESONANCE ENGLISH|Exercise Exercise-2 (Part-3)|33 VideosView PlaylistCHEMICAL BONDING
RESONANCE ENGLISH|Exercise ORGANIC CHEMISTRY(Fundamental Concept )|6 VideosView PlaylistD & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS
RESONANCE ENGLISH|Exercise Match the column|1 VideosView Playlist
RESONANCE ENGLISH-CHEMICAL EQUILIBRIUM-Exercise-2 (Part-4)
- Le Chatelier's Principle If a system at equilibrium is subjected to ...
02:23
|
Play - Le Chatelier's Principle If a system at equilibrium is subjected to ...
01:48
|
Play - For the reaction N(2)(g)+O(2)(g)hArr2NO(g) If pressure id increase...
04:46
|
Play - Effect of temperature on the equilibrium process analysed by using the...
01:59
|
Play - Effect of temperature on the equilibrium process analysed by using the...
03:26
|
Playing Now - Effect of temperature on the equilibrium process analysed by using the...
03:27
|
Play