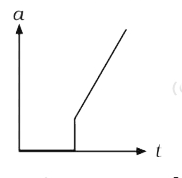
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
DYNAMICS OF A PARTICLE
VMC MODULES ENGLISH|Exercise JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )|31 VideosView PlaylistDYNAMICS OF A PARTICLE
VMC MODULES ENGLISH|Exercise LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )|16 VideosView PlaylistDC CIRCUIT
VMC MODULES ENGLISH|Exercise JEE ADVANCED ARCHIVE|68 VideosView PlaylistELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
VMC MODULES ENGLISH|Exercise IN-CHAPTER EXERCISE-G|10 VideosView Playlist
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-DYNAMICS OF A PARTICLE-JEE Main (Archive) Level - I
- A machine gun fires a bullet of mass 40 g with a velocity 1200 ms^(-1)...
01:59
|
Play - Two masses m1=5kg and m2=4.8kg tied to a string are hanging over a lig...
03:07
|
Play - A particle is acted upon by a force of constant magnitude which is alw...
04:55
|
Play - A block is kept on a frictionless inclined surface with angle of incli...
02:01
|
Play - A particle of mass 0.3 kg subject to a force F=-kx with k=15N//m. What...
02:02
|
Play - A smooth block is released at rest on a 45^@ incline and then slides a...
05:19
|
Play - Consider a car moving on a straight road with a speed of 100m//s. The ...
01:49
|
Play - The upper half of an inclined plane of inclination theta is perfectly ...
03:57
|
Play - A player caught a cricket ball of mass 150g moving at a rate of 20m//s...
03:51
|
Play - A ball of mass 0.2 kg is thrown vertically upwards by applying a force...
02:49
|
Play - A block of mass 'm' is connected to another block of mass 'M' by a spr...
02:11
|
Play - A body of mass m = 3.513 kg is moving along the x-axis with a speed of...
02:02
|
Play - Two fixed frictionless inclined plane making an angle 30^(@) and 60^(@...
04:14
|
Play - A particle of mass m is at rest the origin at time t= 0 . It is subj...
02:31
|
Play - A body starts from rest on a long inclined plane of slope 45^(@) . The...
03:12
|
Play - Two blocks of mass M(1) = 20 kg and M(2) = 12 kg are connected by a ...
02:46
|
Play - A block is placed on a rough horizontal plane. A time dependent horizo...
03:22
|
Playing Now - A block of mass is placed on a surface with a vertical cross section g...
03:07
|
Play - A body with mass 5 kg is acted upon by a force F=(-3 hati+4 hatj)N. If...
03:03
|
Play - A block A of mass 4 kg is placed on another block B of mass 5 kg , and...
03:20
|
Play