Home
Class 12
PHYSICS
A transverse sinusoidal wave of waveleng...

A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:

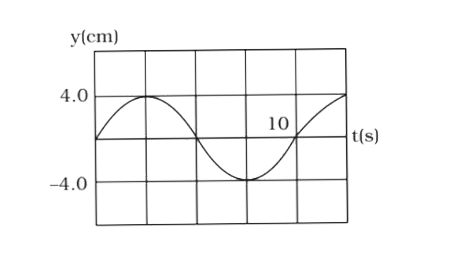
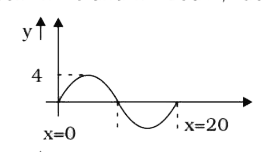
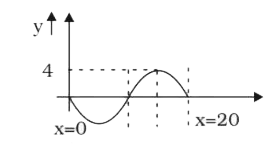
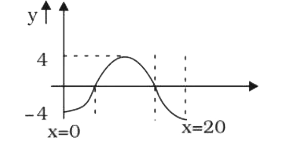
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
B
Wavelength `lamda=20cm`
From the graph given in question,
Amplitude `A=4cm`
Time period, `T=10sec`
`therefore`Frequency, `f=(1)/(T)=0.1Hz`
From given graph
At t=0, velocity of particle at position x=0, along +y direction
`v_(p)=-v((dy)/(dx))`
Slope of wave-curve, `(dy)/(dx)=-(V_(p))/(V)=-(("Positive")/("Positive"))=`negative
And at t=0, at x=0, y=0
So option (B) satisfies the values.
Promotional Banner

Topper's Solved these Questions

  • WAVE MOTION

    VMC MODULES ENGLISH|Exercise JEE MAIN ARCHIVE LEVEL 1|56 Videos

  • WAVE MOTION

    VMC MODULES ENGLISH|Exercise JEE ADVANCED ARCHIVE LEVEL 2|32 Videos

  • WAVE MOTION

    VMC MODULES ENGLISH|Exercise LEVEL-1|75 Videos

  • UNITS, MEASUREMENTS & ERRORS

    VMC MODULES ENGLISH|Exercise IN - CHAPTER EXERCISE - B|10 Videos

  • WORK ENERGY AND POWER

    VMC MODULES ENGLISH|Exercise IMPECCABLE|54 Videos

Similar Questions

Explore conceptually related problems

A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure. Q. The velocity of propagation of the wave is ?

A certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

A certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

A transverse wave is travelling on a string. The equation of the wave

in a sine wave ,postive of different particles at time t=0 is shown in figure. The equation for this wave if it is travelling along postive x -axis can beB

A sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not?

A transverse wave of wavelength 50 cm is travelling towards+vex-axis along a string whose linear density is 0.05 g//cm . The tension in the string is 450 N. At t=0,the particle at x=0 is passing through its mean position wave. The amplitude of the wave is 2.5 cm.

A transverse wave is travelling along a string from right to left. The figure represents the shape of the string at the given instant. A point M has a velocity

A transverse wave of amplitude 2 m, wavelength 4 m and frequency 6 Hz is propagating in a string toward positive y-direction. The equation of the wave may be (y is in m and t is in s)

One end of a long string of linear mass density 10^(-2) kg m^(-1) is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.

VMC MODULES ENGLISH-WAVE MOTION-LEVEL-2
  1. A transverse sinusoidal wave of wavelength 20 cm is moving along a str...

    Text Solution

    |

  2. A transverse sinusoidal wave of wavelength 20 cm is moving along a str...

    Text Solution

    |

  3. A transverse sinusoidal wave of wavelength 20 cm is moving along a str...

    Text Solution

    |

  4. Sound wave is travellimg along positive x -direction . Displacement...

    Text Solution

    |

  5. The equation of a transverse mechanical wave propagating along the 'x'...

    Text Solution

    |

  6. The loudspeaker diaphragmm 0.2 m in diameter is vibrating at 1 kHz wit...

    Text Solution

    |

  7. The figure represents two snaps of a travelling wave on a string of ma...

    Text Solution

    |

  8. The figure represents two snaps of a travelling wave on a string of ma...

    Text Solution

    |

  9. For four sine waves, moving on a string along positive x-direction, di...

    Text Solution

    |

  10. A 10 m long horizontal stainless steel wire AB of mass 1 kg whose end ...

    Text Solution

    |

  11. A wave y= 3mm sin (2pix-200 pit) is Propagating in the left strin...

    Text Solution

    |

  12. The equation of a wave distrubance is a given as y= 0.02 sin ((pi)/(...

    Text Solution

    |

  13. A wire of density 9xx10^(-3) kg cm^(-3) is stretched between two c...

    Text Solution

    |

  14. Incident wave y= A sin (ax + bt+ pi/2) is reflected by an obstacle at ...

    Text Solution

    |

  15. Incident wave y= A sin (ax + bt+ pi/2) is reflected by an obstacle at ...

    Text Solution

    |

  16. Incident wave y= A sin (ax + bt+ pi/2) is reflected by an obstacle at ...

    Text Solution

    |

  17. An aluminium wire and a steel wire of same cross-sectional of 10^(-2)c...

    Text Solution

    |

  18. the frequency of a sonometer wire is 10 Hz. When the weight producing ...

    Text Solution

    |

  19. Following is given the eqution of a stationary wave (all in SI units) ...

    Text Solution

    |

  20. Fig. shows a wave motion in which displacements of particles at an ins...

    Text Solution

    |