Natural frequency of a system is called its fundamental frequency, whose wavelength is denoted as `lamda_(f)`. Match each system with statements given in Column-II describing the nature and wavelength of the standing waves.
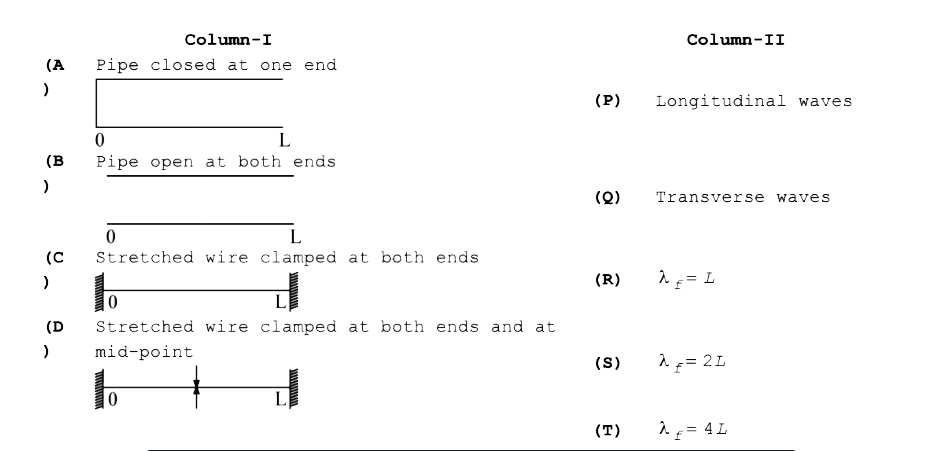
Natural frequency of a system is called its fundamental frequency, whose wavelength is denoted as `lamda_(f)`. Match each system with statements given in Column-II describing the nature and wavelength of the standing waves.
Text Solution
Verified by Experts
The correct Answer is:
A, B, C, D
A-P,T,B-P,S,C-Q,S,D-Q,R
(A) Sound wave are longitudinal waves `(lambda_f)/2=L implieslambda_f=4L`
(B) (A) Sound wave are longitudinal waves `(lamda_f)/2=L implies lambda_f=2L`
( c )string wave are transervse wave `(lambda_f)/2=L implies lambda_f=L`
(D) string wave are transverse waves `(lambda_f)/2=L implies lambda_f=L`
(A) Sound wave are longitudinal waves `(lambda_f)/2=L implieslambda_f=4L`
(B) (A) Sound wave are longitudinal waves `(lamda_f)/2=L implies lambda_f=2L`
( c )string wave are transervse wave `(lambda_f)/2=L implies lambda_f=L`
(D) string wave are transverse waves `(lambda_f)/2=L implies lambda_f=L`
|
Topper's Solved these Questions
WAVE MOTION
VMC MODULES ENGLISH|Exercise JEE ADVANCED ARCHIVE LEVEL 2 (NUMERICAL VALUE TYPE)|21 VideosWAVE MOTION
VMC MODULES ENGLISH|Exercise JEE ADVANCED ARCHIVE LEVEL 2 (FILL IN THE BLANKS)|17 VideosWAVE MOTION
VMC MODULES ENGLISH|Exercise JEE ADVANCED ARCHIVE LEVEL 2 (PARAGRAPH TYPE)|6 VideosUNITS, MEASUREMENTS & ERRORS
VMC MODULES ENGLISH|Exercise IN - CHAPTER EXERCISE - B|10 VideosWORK ENERGY AND POWER
VMC MODULES ENGLISH|Exercise IMPECCABLE|54 Videos
Similar Questions
Explore conceptually related problems
A harmonic wave has been set up on a very long string which travels along the length of string. The wave has frequency of 50 Hz. Amplitude 1 cm and wavelength 0.5 m. for the above described wave. Statement (i): time taken by a point on the string to travel a distance of 8 m along the length of string is 0.32 s. Statement (ii): time taken by a point in the string to travel a distance of 8m, once the wave has reached at that point and sets it into motion is 0.32 s.
A dence collection of equal number of electrona and positive ions is called netural plasma. Certain solids contianing fixed positive ions surroundedby free electrons can be treated as neytral plasma. Let 'N' be the numbrer density of free electrons, each of mass ' m '. When the elctrons are subjected to an eletric field, they are displaced relatively away from the heavy positive ions. if the electric field becomes zero, the electrons begin to oscillate about the positive ions with a natural angular frequency ' omega_(P)' which is called the plasma frequency. to sustain the oscillations, a time varying electric field needs to be applied that has an angular frequrncy omega , where a part of the energy is absorbed and a part of it is reflected. As omega approaches omega_(p) all the free electrons are set to resonance together and all the energy is reflected. this is the explaination of high reflectivity of metals. (2) Estimate the wavelength at which plasma reflection will occur for a metal having the density of electrons N~~ 4 xx 10^(27)m^(-3) . Taking epsilon_(0) = 10^(11) and mass m~~ 10^(-30) , where these quantities are in proper SI units.
Knowledge Check
Optical communication system having an operating wavelength lambda metre can use only x % of its source frequency as its channel band width. The system is to be used for transmitting T.V signals requiring a band width of F hertz. How many channels can this system transmit simultaneously? Show graphically how this number of channels varies with operating wavelength of the system.
Optical communication system having an operating wavelength lambda metre can use only x % of its source frequency as its channel band width. The system is to be used for transmitting T.V signals requiring a band width of F hertz. How many channels can this system transmit simultaneously? Show graphically how this number of channels varies with operating wavelength of the system.
A
`lambdaF//Cx`
B
`2_(Cx)//100lambdaF`
C
` cx//50lambdaF`
D
`cx//100lambdaF`
Similar Questions
Explore conceptually related problems
A 160 g rope 4 m long is fixed at one end and tied to a light string of the same length at the other end. Its tension is 400 N. (a) What are the wavelength of the fundamental and the first two overtones? (b) What are the frequencies of these standing waves? [Hint : In this case, fixed end is a node and the end tied with the light string is antinode.]
When a particle is restricted to move along x-axis between x=0 and x=a , where alpha if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a . The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=(p^2)/(2m) . Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...( n=1 , called the ground state) corresponding to the number of loops in the standing wave. Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=alpha . Take h=6.6xx10^(-34)Js and e=1.6xx10^(-19) C. Q. If the mass of the particle is m=1.0xx10^(-30) kg and alpha=6.6nm , the energy of the particle in its ground state is closest to
When a particle is restricted to move along x-axis between x=0 and x=a , where alpha if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a . The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=(p^2)/(2m) . Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...( n=1 , called the ground state) corresponding to the number of loops in the standing wave. Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=alpha . Take h=6.6xx10^(-34)Js and e=1.6xx10^(-19) C. Q. The allowed energy for the particle for a particular value of n is proportional to
When a particle is restricted to move along x-axis between x=0 and x=a , where alpha if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a . The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=(p^2)/(2m) . Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...( n=1 , called the ground state) corresponding to the number of loops in the standing wave. Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=alpha . Take h=6.6xx10^(-34)Js and e=1.6xx10^(-19) C Q. The speed of the particle that can take discrete values is proportional to
A : All electromagnetic waves travel through vacuum with same speed but they have different wavelength or frequency. R : The wavelength of the electromagnetic waves is often correlated with and characteristic size of the system that produces and radiates them.
A transverse sinusoidal wave of amplitude a, wavelength lamda and frequency f is travelling on a stretched string. The maximum speed of any point on the string is v/10, where v is the speed of propagation of the wave. If a = 10^(-3) m and y = 10m/s, then lamda and f are given by
In each of the four situations of column-I , a stretched string or an organ pipe is given along with the required data. In case of strings the tension in string is T=102.4 N and the mass per unit length of string is 1g/m. Speed of sound in air is 320 m/s. Neglect end corrections.The frequencies of resonance are given in column-II.Match each situation in column-I with the possible resonance frequencies given in Column-II.