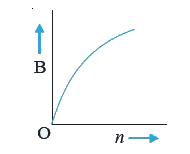
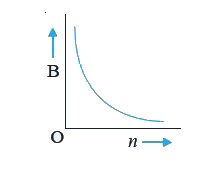
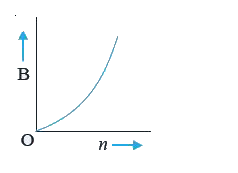
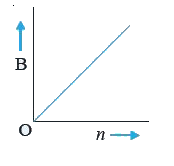
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
MOVING CHARGES & MAGNETISM
VMC MODULES ENGLISH|Exercise PRACTICE EXERCISE 10|5 VideosMOVING CHARGES & MAGNETISM
VMC MODULES ENGLISH|Exercise PRACTICE EXERCISE6|1 VideosMOVING CHARGES & MAGNETISM
VMC MODULES ENGLISH|Exercise PRACTICE EXERCISE 8|5 VideosMotion in Two Dimensions
VMC MODULES ENGLISH|Exercise MCQ|2 VideosPROPERTIES OF MATTER
VMC MODULES ENGLISH|Exercise JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)|1 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-MOVING CHARGES & MAGNETISM -PRACTICE EXERCISE 9
- A thin wire of length l is carrying a constant current. The wire is be...
Text Solution
|
- The resistance of an ideal voltmeter is
Text Solution
|
- Magnetic lines of force
Text Solution
|
- A magnet of magnetic moment 50 hat(i) A-m^(2) is placed along the x-ax...
Text Solution
|
- At what positions, the neutral points will lie for a bar magnet when m...
Text Solution
|