Home
Class 10
MATHS
In general, given a polynomial p(x) of d...

In general, given a polynomial p(x) of degree n, the graph of y = p(x) intersects the x-axis atmost n points. Therefore, a polynomial p(x) of degree n has atmost n zeroes:

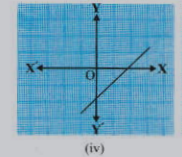
Answer

Step by step text solution for In general, given a polynomial p(x) of degree n, the graph of y = p(x) intersects the x-axis atmost n points. Therefore, a polynomial p(x) of degree n has atmost n zeroes: by MATHS experts to help you in doubts & scoring excellent marks in Class 10 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • PAIR OF LINEAR EQUATIONS IN TWO VARIABLES

    PSEB|Exercise EXERCISE |78 Videos

  • PROBABILITY

    PSEB|Exercise EXAMPLE|21 Videos

Similar Questions

Explore conceptually related problems

f(x) is a polynomial of degree

Find the zero of the polynomial: p(x)=x-4

Find the zeroes of the polynomial: p(x)=x-4

The graph of y = p (x) is given. Find the number of zeroes of p (x)

Find a zero of the polynomial p(x) = 2x + 1.

Verify that 6 is a zero of the polynomial p(x)=x-6

If 'a' is a zero of the polynomial p(x), then p(a)=1.

The graphs of y = p(x) arc giver in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x),in each ease

Verify that: -5 is a zero of the polynomial p(x)=x+5?

The graphs of y - p (x) are given in Fig. below, for some polynomials p(x). Find the number of zeroes of p (x), in each case. .

Home
Profile