Gauss.s law
Proof of Gauss.s law for spherically symmetric surface Consider an isolated positive point charge q. Let S be the spherical Gaussian surface of radius r centred on q.
Let an area element d S on surface S.
`therefore` Electric flux through an area element dS on the surface S is
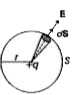
`d phi= E.dS= (1)/(4pi epsi_(0)) .(q)/(r^(2)) hat(r ) (dS hat(n))`
As the unit vectors `har(r ) and hat(n)` both are in the same direction, so `hat(r ).hat(n)= 1.1 cos 0^(@)=1`
`rArr d phi = (1)/(4pi epsi_(0)).(q dS)/(r^(2))`
Total electric flux through the spherical surface is `phi_(E )= underset(S)oint d phi= (1)/(4pi epsi_(0)) (q)/(r^(2)) underset(S)oint dS`
`=(1)/(4pi epsi_(0)) .(q)/(r^(2)) .4pi r^(2)= (q)/(epsi_(0)) rArr phi_(E )= (q)/(epsi_(0))`
Electric field intensity due to a charged plane lamina. Let `sigma` be the surface charge density of the sheet. From symmetry, E on either side of the sheet must be perpendicular to the plane of the sheet having same magnitude at all points equidistant from the sheet.
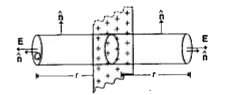
We take a cylinder of cross-sectional area A and length 2r as the Gaussian surface. On the curved surface of the cylinder, E and `hat(n)` are perpendicular to each other. Therefore, flux through curved surface is zero. Flux through the flat surfaces.
`=EA + EA= 2EA`
where, A= area of each flat surface.
`therefore` Total electric flux over the entire surface of cylinder, `phi_(E)= 2EA`
Total charge enclosed by the cylinder, `q= sigma A`
According to Gauss.s law, `phi_(E)= (q)/(epsi_(0)) rArr 2EA= (sigma A)/(epsi_(0)) rArr E= (sigma)/(2epsi_(0))`
E is independent of r, the distance of the point from the plane charged sheet. It means that the electric field intensity is same for all points close to the plane sheet of charge. E at any point is directed away from the sheet in case of positive charge and directed towards the sheet in case of negative charge.

