Recommended Questions
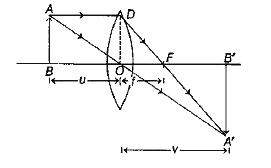
- Derive the formula (1)/(v)-(1)/(u)=(1)/(f) for a thin convex v u f le...
Text Solution
|
Playing Now - A plano convex lens is made of glass of refractive index 1.5. The radi...
01:59
|
Play - The radius of curvature of the curved surface of a plano-convex lens i...
03:29
|
Play - The radius of curvature of the face of plano-convex lens is 12cm and i...
Text Solution
|
Play - Find the focal length of plano convex lens, when its radius of curvatu...
Text Solution
|
Play - Find the radius of curvature of the convex surface of a plano-convex l...
02:54
|
Play - A thin plano-convex lens acts like a concave mirror of focal length 0....
03:30
|
Play - A thin plano -convex lens acts like a concave mirror of focal length 0...
Text Solution
|
Play - Find the radius of curvature of the convex surface of a plano-convex l...
Text Solution
|
Play