Home
Class 14
MATHS
There circle C1,C2 and C3 with radii r1,...

There circle `C_1,C_2` and `C_3` with radii `r_1`,`r_2` and `r_3` (where `r_1 तीन वृत्त`C_1,C_2` तथा `C_3` जिनको त्रिज्याएँ `r_1`,`r_2` तथा `r_3` है, (जहाँ `r_1

A

`sqrt((r_1r_3))`

B

`(r_1+r_3)//2`

C

`(2r_1r_2)//(r_1+r_2)`

D

`sqrt((r_1+r_3))`

Text Solution

Verified by Experts

Promotional Banner

Topper's Solved these Questions

  • 2017 TIER-II PAPER(8)

    CHAMPION PUBLICATION|Exercise EXERCISE|100 Videos

  • 2018 TIER-II PAPER(4)

    CHAMPION PUBLICATION|Exercise EXERCISE|100 Videos

Similar Questions

Explore conceptually related problems

Three circles with centres C_(1),C_(2) and C_(3) and radii r_(1),r_(2) and r_(3) where *r_(-)1

Three circle C_(1),C_(2)andC_(3) with radii r_(1),r_(2) and r_(3) (where r_(1)ltr_(2)ltr_(3) ) are placed as shown in the given figure. What is the value of r_(2) ?

Consider a series of 'n' concentric circles C_1, C_2, C_3, ....., C_n with radii r_1, r_2, r_3, ......,r_n respectively, satisfying r_1 > r_2 > r_3.... > r_n and r_1= 10. The circles are such that the chord of contact of tangents from any point on C_1 to C_(i+1) is a tangent to C_(i+2) (i = 1, 2, 3,...). Find the value of lim_(n->oo) sum_(i=1)^n r_1, if the angle between the tangents from any point of C_1 to C_2 is pi/3.

Three circles C_(1),C_(2),C_(3) with radii r_(1),r_(2),r_(3)(r_(1)ltr_(2)ltr_(3)) respectively are given as r_(1)=2 , and r_(3)=8 they are placed such that C_(2) lines to the right of C_(1) and touches it externally C_(3) lies ot the right of C_(2) and touches it externally. There exist two stratight lines each of whic is a direct common tangent simultaneously to all the three circles then r_(2) is equal to

If A=[[1, 2, -1], [3, -2, 5]] , then first R_1 harr R_2 and then C_1 to C_1+2C_3 on A gives

Prove that : (r_1+r_2) tan (C )/(2) = (r_3- r) cot ( C)/(2) = c

If A = [[1,-1,3] , [2,1,0] , [3,3,1]] then apply R_1 rarr R_2 and then C_1 rarr C_1 +2C_3 on A

CHAMPION PUBLICATION-2017 TIER-II PAPER(9)-EXERCISE
  1. There are 8 equidistant points A, B, C, D, E, F, G and H (in same orde...

    Text Solution

    |

  2. In the given figure, O is the centre of the circle and angle QOR= 50^@...

    Text Solution

    |

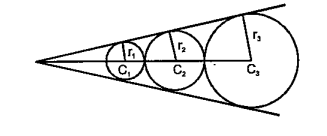
  3. There circle C1,C2 and C3 with radii r1,r2 and r3 (where r1 <r2 <r3) a...

    Text Solution

    |

  4. An equilateral triangle of area 300cm^(2) is cut from its three vertic...

    Text Solution

    |

  5. In the given figure, PQR is an equilateral triangle with side as 12cm....

    Text Solution

    |

  6. ABCD is a rectangle P is point on the side AB as shown in the given fi...

    Text Solution

    |

  7. In the given figure PQRSTU is a regular hexagon of side 12 cm. what is...

    Text Solution

    |

  8. In the given figure, ABCD is a square, BCXYZ is a regular pentagon and...

    Text Solution

    |

  9. In the given figure, 3 semicircles are drawn on three sides of triangl...

    Text Solution

    |

  10. The sum of radii of the two circles is 91 cm and the difference betwee...

    Text Solution

    |

  11. A right triangular prism has equilateral triangle as its base. Side of...

    Text Solution

    |

  12. The height of a cone is 45cm. It is cut at a height of 15cm from its b...

    Text Solution

    |

  13. The ratio of the curved surface area and total surface area of a right...

    Text Solution

    |

  14. The radius and height of a solid cylinder are increased by 2% each. Wh...

    Text Solution

    |

  15. A sphere of radius 21 cm is cut into 8 identical parts by 3 cuts (1 cu...

    Text Solution

    |

  16. Two identical hemispheres of maximum possible size are cut from a soli...

    Text Solution

    |

  17. Identical cubes of largest possible size are cut from a solid cuboid o...

    Text Solution

    |

  18. A regular triangular pyramid is cut by 2 planes which are parallel to ...

    Text Solution

    |

  19. What is the value of [(cos 7A +cos 5A) div (sin 7A -sin 5A)]? [(cos...

    Text Solution

    |

  20. What is the value of [1 - sin(90 -2A)|//[1 + sin (90 + 2A)]? [1 - si...

    Text Solution

    |