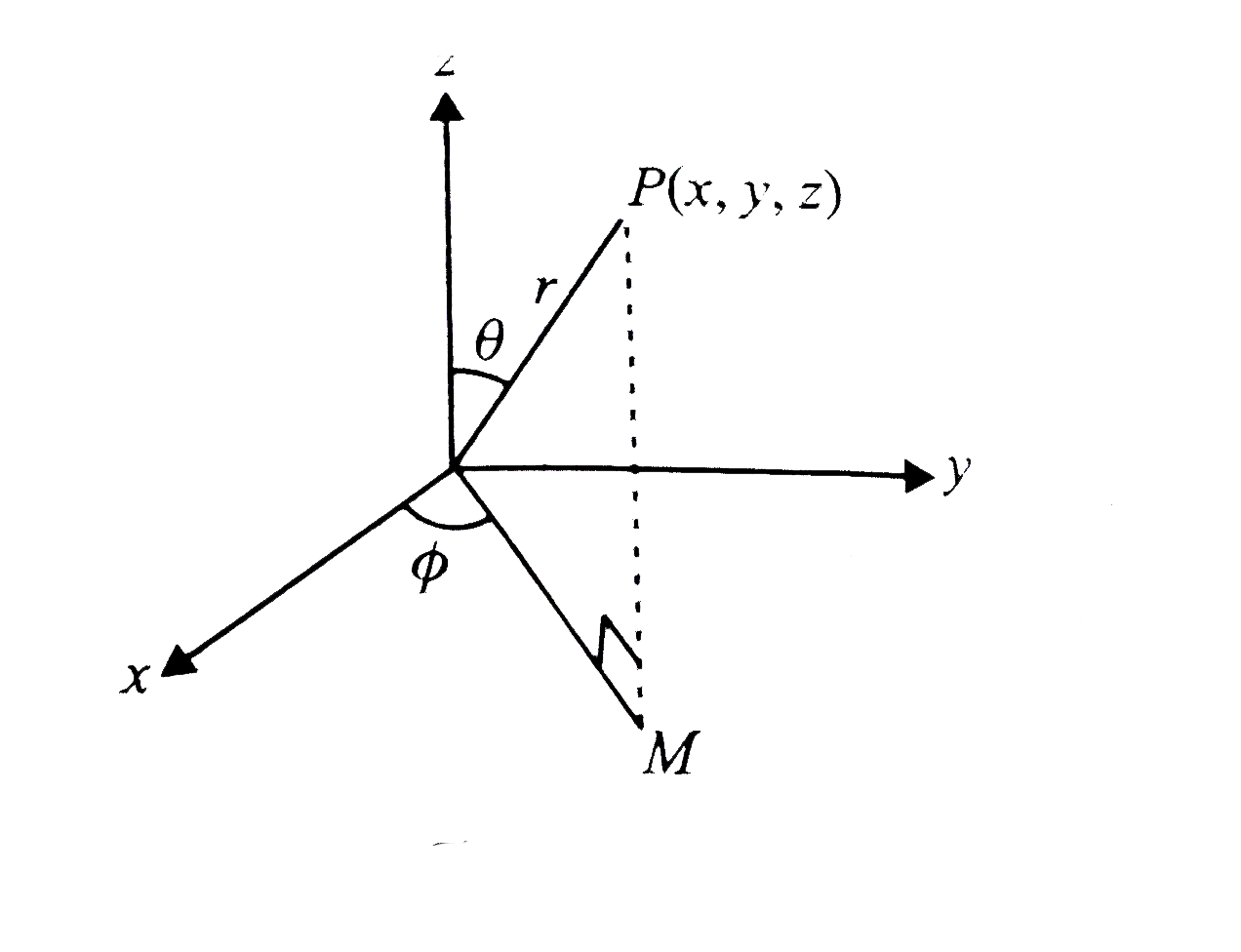A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
THREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise Exercise (Reasoning Questions)|10 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise Exercise (Comprehension)|12 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE|Exercise Exercise (Single)|86 VideosTHREE DIMENSIONAL GEOMETRY
CENGAGE|Exercise Question Bank|12 VideosTRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
CENGAGE|Exercise Question Bank|4 Videos
Similar Questions
Explore conceptually related problems
CENGAGE-THREE-DIMENSIONAL GEOMETRY -Exercise (Multiple)
- Let P M be the perpendicular from the point P(1,2,3) to the x-y plane....
Text Solution
|
- Find vec a . vec b, when vec a = hat i +3 hat j + hat k and vec b =...
Text Solution
|
- If the planes vecr.(hati+hatj+hatk)=q(1),vecr.(hati+2ahatj+hatk)=q(2)a...
Text Solution
|
- A line with direction cosines proportional to 1,-5, a n d-2 meets l...
Text Solution
|
- Let P=0 be the equation of a plane passing through the line of inte...
Text Solution
|
- about to only mathematics
Text Solution
|
- Consider the planes 3x-6y+2z+5=0a n d4x-12+3z=3. The plane 67 x-162 y+...
Text Solution
|
- If the lines (x-2)/(1)=(y-3)/(1)=(z-4)/(-k) and (x-1)/(k)=(y-4)/...
Text Solution
|
- The equations of the plane which passes through (0,0,0) and which i...
Text Solution
|
- The x-y plane is rotated about its line of intersection with the y-...
Text Solution
|
- The equation of the plane which is equally inclined to the lines (x...
Text Solution
|
- Which of the following lines lie on the plane x+2y-z+4=0? a. (x-1)...
Text Solution
|
- If the volume of tetrahedron A B C D is 1 cubic units, where A(0,1,...
Text Solution
|
- A rod of length 2 units whose one end is (1,0,-1) and other end tou...
Text Solution
|
- Find the angle between the line (x-2)/(3)=(y-1)/(-1)=(z-3)/(2)" and th...
Text Solution
|
- The equation of the line throgh the point veca parallel to the plane v...
Text Solution
|
- about to only mathematics
Text Solution
|