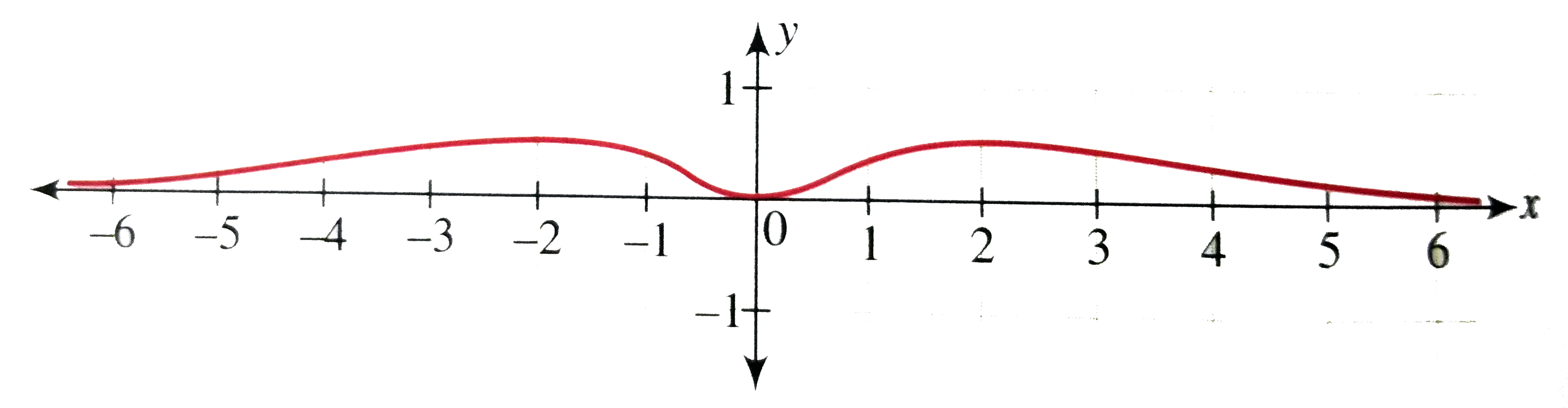
Text Solution
Verified by Experts
|
Topper's Solved these Questions
CURVE TRACING
CENGAGE|Exercise Exercise|24 VideosView PlaylistCROSS PRODUCTS
CENGAGE|Exercise DPP 2.2|13 VideosView PlaylistDEFINITE INTEGRATION
CENGAGE|Exercise JEE Advanced Previous Year|38 VideosView Playlist
Similar Questions
Explore conceptually related problems
CENGAGE-CURVE TRACING-Exercise
- Draw the graph of f(x) = x^(2)e^(-|x|) i) Find the point of maxima/m...
08:26
|
Playing Now - Draw the graph of y=sin^(2)x-cosx
03:36
|
Play - Draw and discuss the graph of f(x) = x+sqrt(x-1)
04:17
|
Play - Draw the graph of y=sqrt(1+x^(2))-x
05:41
|
Play - Draw the graph of y=(sqrt(x^(2)+1)-sqrt(x^(2)-1))
05:36
|
Play - Draw the graph of y=sqrt(x)/(x-1)
03:54
|
Play - Draw the graph of the relation y=|x|sqrt(1-x^(2))
05:36
|
Play - Draw the graph of y=sqrt((1-x)/(1+x)).
02:35
|
Play - Draw the graph of |x|+|y|=1+x.
01:28
|
Play - Draw the graph of y=(3sqrt(x^(2)+1))/(x-1)
05:28
|
Play - Draw and discuss the graph of the function f(x) = e^(1//x)
03:36
|
Play - Draw the graph of y=1/(log(e)x)
03:55
|
Play - Draw the graph of y=1/(log(e)x)
03:55
|
Play - Draw the graph of f(x)=e^(-x^(2)). Discuss the concavity of the graph.
02:33
|
Play - Draw the graph of f(x) = e^(x)/(1+e^(x)). Also find the point of infle...
03:37
|
Play - Draw the graph of the function f(x)=x^2
02:51
|
Play - Draw the graph of y=x//"ln "x
05:13
|
Play - Draw the graph of y=(log(e)x)^(2)
03:03
|
Play - Draw the graph of y=log(e)(x^(2)-1)
02:24
|
Play - Draw and graph of f(x) = (4log(e)x)/(x^(2)). Also find the range.
04:54
|
Play - Draw the graph of the relation y^(2)=x^(5)(2-x)
07:25
|
Play