Recommended Questions
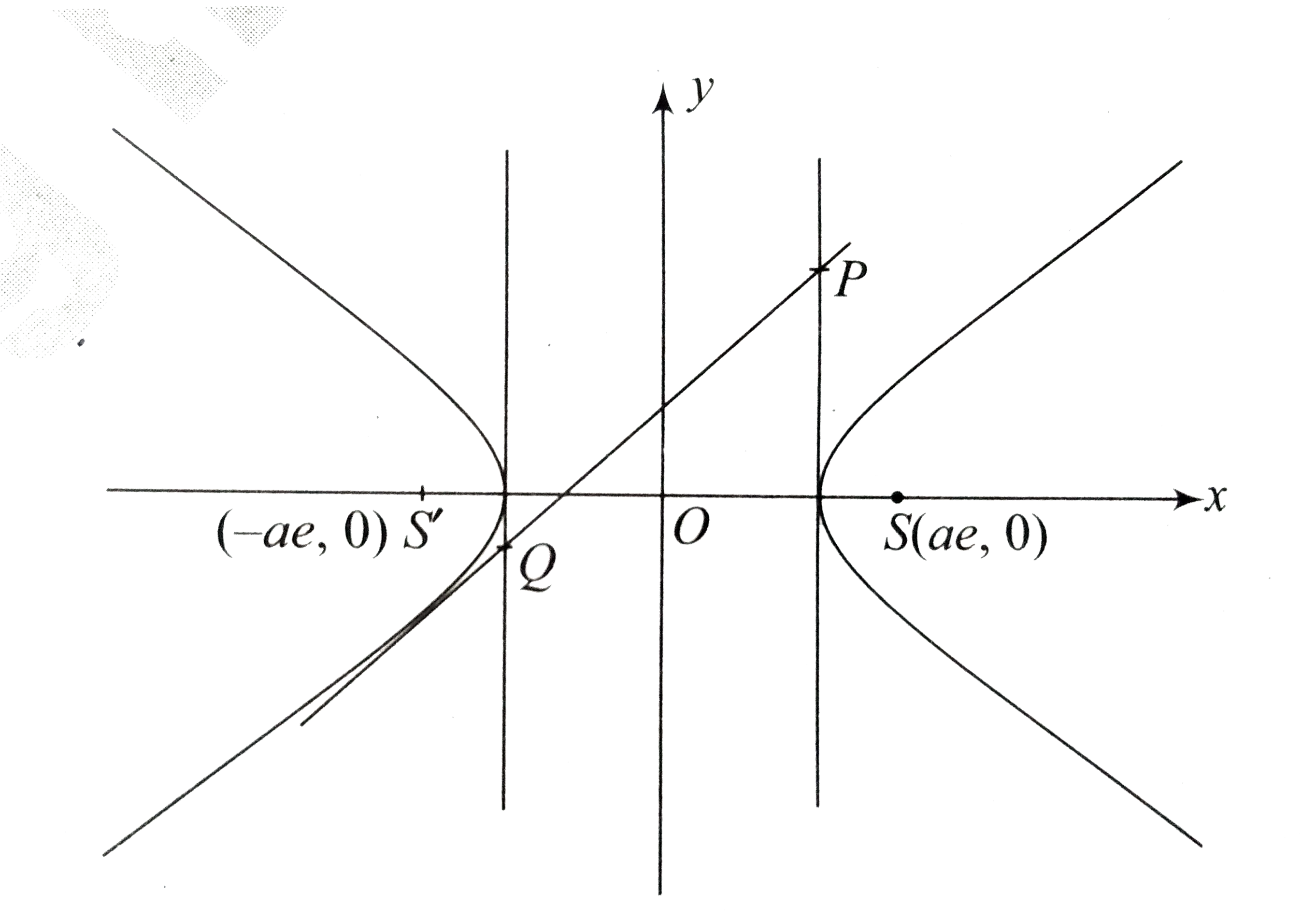
- A tangent is drawn at any point on the hyperbola (x^(2))/(a^(2))-(y^(2...
09:24
|
Playing Now - tangent is drawn at point P(x(1),y(1)) on the hyperbola (x^(2))/(4)-y^...
04:58
|
Play - Tangents are drawn to the hyperbola 4x^2-y^2=36 at the points P and Q....
05:31
|
Play - Tangents are drawn to x^2 + y^2 = 1 from any arbitrary point P on the ...
06:16
|
Play - A tangent is drawn at any point on the hyperbola (x^(2))/(a^(2))-(y^(2...
Text Solution
|
Play - Statement-1 : Tangents drawn from the point (2,-1) to the hyperbola x^...
03:55
|
Play - Tangents at any point P is drawn to hyperbola (x^(2))/(a^(2)) - (y^(2)...
09:24
|
Play - Show that the tangents drawn at those points of the ellipse (x^(2))/(a...
06:33
|
Play - A line through the origin meets the circle x^(2) +y^(2) =a^(2) at P ...
Text Solution
|
Play