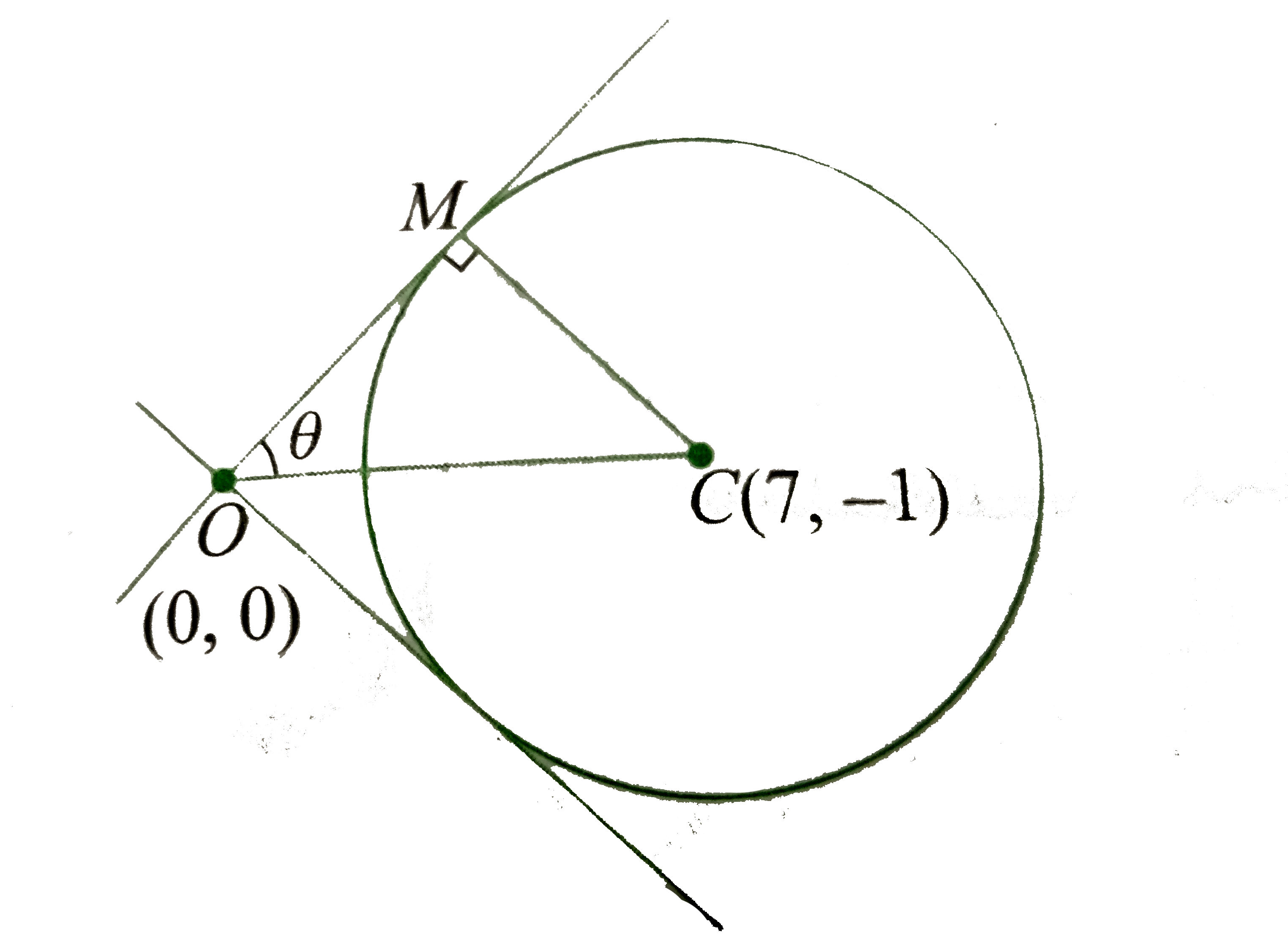Home
Class 12
MATHS
Find the angle between the two tangents ...

Find the angle between the two tangents from the origin to the circle `(x-7)^2+(y+1)^2=25`

Text Solution

Verified by Experts

The correct Answer is:
`90^(@)`
Centre of the circle is C(7,-1) and radius , `CM=5`.

`OC =sqrt(7^(2)+ (-1)^(2))=5sqrt(2)`
`:. sin theta =(CM)/(OC)=(5)/(5sqrt(2))=(1)/(sqrt(2))`
`implies theta =45^(@)`
Hence, angle between tangents is `90^(@)`.
Promotional Banner

Topper's Solved these Questions

Similar Questions

Explore conceptually related problems

Find the angle between the tangents drawn from the origin to the parabolas y^2=4a(x−a) (a) 90^@ (b) 30^@ (c) tan^-1 (1/2) (d) 45^@

Find the angle between the pair of tangents from the point (1,2) to the ellipse 3x^2+2y^2=5.

Find the angle between the tangents drawn from (1, 3) to the parabola y^2=4xdot

If S_(1)=alpha^(2)+beta^(2)-a^(2) , then angle between the tangents from (alpha, beta) to the circle x^(2)+y^(2)=a^(2) , is

Find the equation of the two tangents from the point (1,2) to the hyperbola 2x^(2)-3y^2=6

The equation of tangents drawn from the origin to the circle x^2+y^2-2rx-2hy+h^2=0

Find the angle between the straight lines joining the origin to the point of intersection of 3x^2+5x y-3y^2+2x+3y=0 and 3x-2y=1

Find the equation of the tangent at the endpoints of the diameter of circle (x-a)^2+(y-b)^2=r^2 which is inclined at an angle theta with the positive x-axis.

Find the length of the tangent from (2,-3) to the circle x^(2) + y^(2) -8y -9y + 12=0

Find the equation of the common tangent in the first quadrant of the circle x^2+y^2=16 and the ellipse x^2/25+y^2/4=1 .Also find the length of the intercept of the tangent between the coordinates axes.

CENGAGE-CIRCLE -Exercise 4.3
  1. Find the angle between the two tangents from the origin to the circle ...

    Text Solution

    |

  2. If the join of (x1,y1) and (x2,y2) makes on obtuse angle at (x3,y3), t...

    Text Solution

    |

  3. about to only mathematics

    Text Solution

    |

  4. The locus of centre of a circle which passes through the origin and cu...

    Text Solution

    |

  5. The least distance of the line 8x -4y+73=0 from the circle 16x^2+16y^...

    Text Solution

    |

  6. If the length tangent drawn from the point (5, 3) to the circle x^2...

    Text Solution

    |

  7. The length of the tangent from any point on the circle to the circle (...

    Text Solution

    |

  8. Find the locus of a point which moves so that the ratio of the lengths...

    Text Solution

    |

  9. Find the length of the tangent drawn from any point on the circle x^2+...

    Text Solution

    |

  10. A tangent is drawn to each of the circles x^2+y^2=a^2 and x^2+y^2=b^2d...

    Text Solution

    |

  11. The equation of chord AB of the circle x^2+y^2=r^2 passing through t...

    Text Solution

    |

  12. If a circle passes through the point of intersection of the lines lamb...

    Text Solution

    |

  13. Two variable chords A Ba n dB C of a circle x^2+y^2=r^2 are such that ...

    Text Solution

    |

  14. If the circle x^2+y^2-4x-8y-5=0 intersects the line 3x-4y=m at two dis...

    Text Solution

    |

  15. (C) 2 45. Three concentric circles of which the biggest is x^2+ y^2= 1...

    Text Solution

    |

  16. Find the middle point of the chord of the circle x^2+y^2=25 intercepte...

    Text Solution

    |

  17. Find the locus of the midpoint of the chord of the circle x^2+y^2-2x-2...

    Text Solution

    |

  18. about to only mathematics

    Text Solution

    |