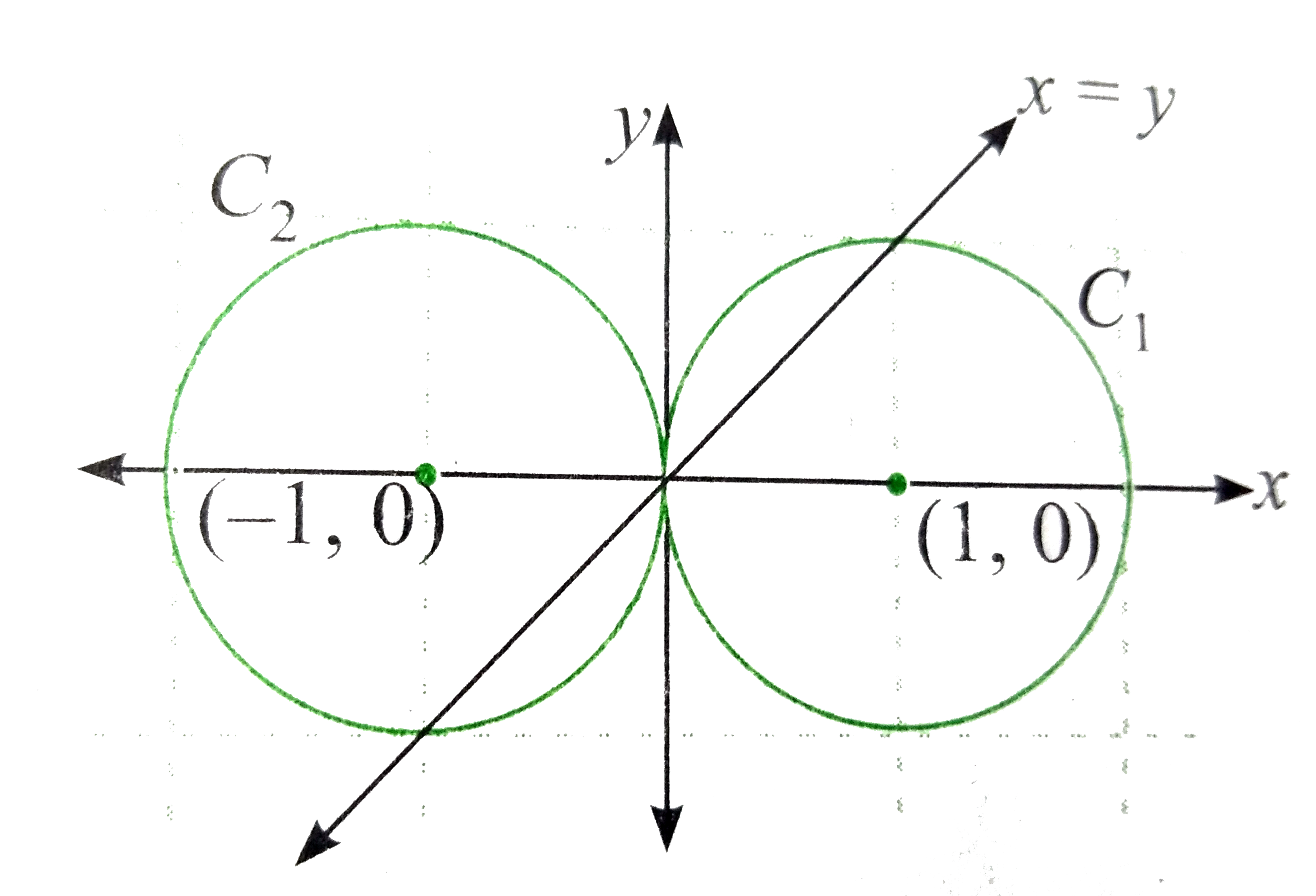
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CIRCLE
CENGAGE|Exercise Exercise (Numerical)|18 VideosView PlaylistCIRCLE
CENGAGE|Exercise JEE Main Previous Year|10 VideosView PlaylistCIRCLE
CENGAGE|Exercise Exercise (Comprehension)|46 VideosView PlaylistBINOMIAL THEOREM
CENGAGE|Exercise Comprehension|11 VideosView PlaylistCIRCLES
CENGAGE|Exercise Question Bank|16 VideosView Playlist
Similar Questions
Explore conceptually related problems