Home
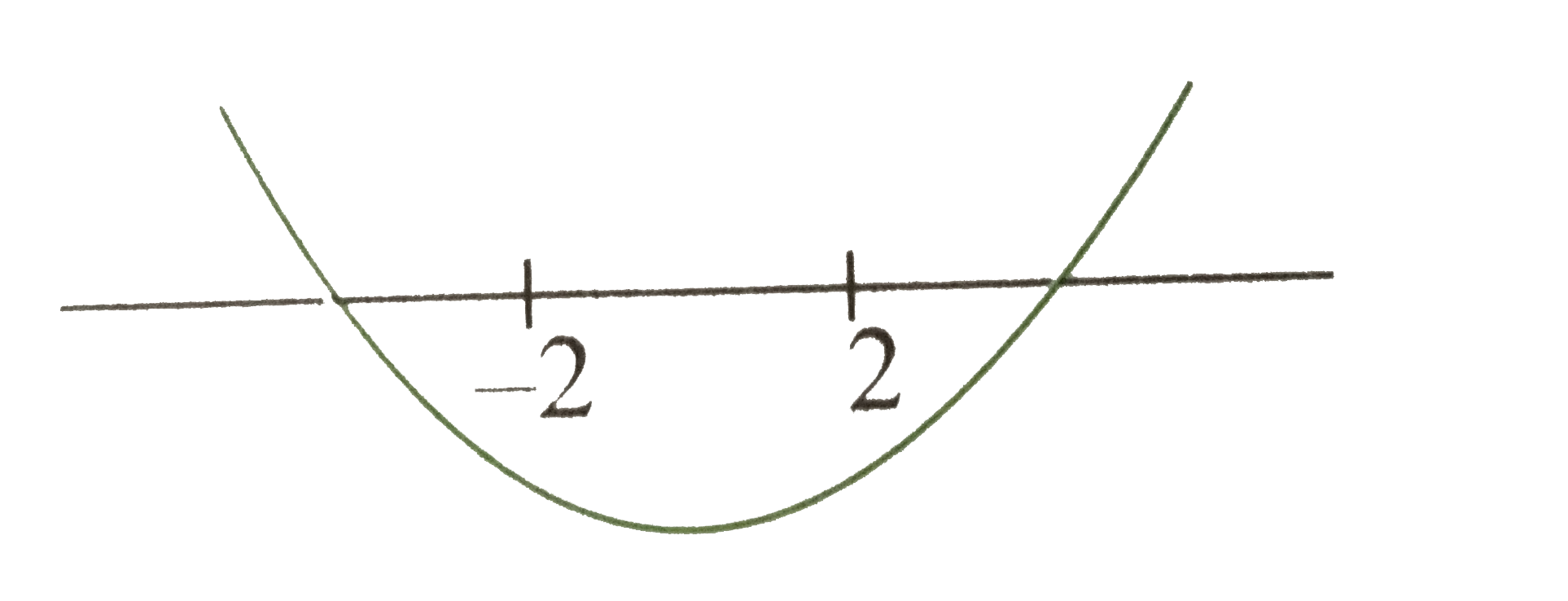
Class 12
MATHS
ax^2 + bx + c = 0(a > 0), has two roots ...

`ax^2 + bx + c = 0(a > 0),` has two roots `alpha and beta` such `alpha < -2 and beta > 2,` then

A

` a + |b| + c lt 0 `

B

` c lt 0, b^(2) - 4ac gt 0 `

C

`4a + 2 |b| + c lt 0 `

D

` 9a - 3 |b| + c lt 0 `

Text Solution

Verified by Experts

The correct Answer is:
1,2,3
` f(x) = ax^(2) + bx + c `
` f(0) = c lt 0 , D gt 0 `
`rArr b^(2) - 4ac gt 0 `
`f(1) lt 0 and f(-1) lt 0 `
`rArr a - |b| + c lt 0 `
` f(2) lt 0 and f(-2) lt 0 `
`rArr 4a - 2 |b| + c lt 0 `

Nothing can be said about ` f(3) or f(-3)` , whether it is positive
or negative .
Promotional Banner

Topper's Solved these Questions

  • THEORY OF EQUATIONS

    CENGAGE|Exercise Exercise (Comprehension)|37 Videos

  • THEORY OF EQUATIONS

    CENGAGE|Exercise Exercise (Matrix)|6 Videos

  • THEORY OF EQUATIONS

    CENGAGE|Exercise Exercise (Single)|89 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise JEE Advanced Previous Year|4 Videos

  • THREE DIMENSIONAL GEOMETRY

    CENGAGE|Exercise Question Bank|12 Videos

Similar Questions

Explore conceptually related problems

If the equation ax^2 + bx + c = 0 ( a gt 0) has two roots alpha and beta such that alpha 2 , then

If the equation ax^(2)+bx+c=0, a gt 0 , has two distinct real roots alpha" and "beta such that alpha lt -5" and "beta gt 5 , then

Consider a quadratic equation ax^2 + bx + c = 0 having roots alpha, beta . If 4a + 2b + c > 0,a-b+c 0 then |[alpha] + [beta]| can be {where [] is greatest integer}

If tan alpha and tan beta are the roots of x^2 + ax + b = 0 , where a ne 0 then sin (alpha + beta) sec alpha sec beta is equal to ……………….

Let f(x) = ax^(2) + bx + c, a != 0 and Delta = b^(2) - 4ac . If alpha + beta, alpha^(2) + beta^(2) and alpha^(3) + beta^(3) are in GP, then

One of the roots of ax^(2) + bx + c = 0 is greater than 2 and the other is less than -1. If the roots of cx^(2) + bx + a = 0 are alpha and beta , then

If a, b and c are in geometric progression and the roots of the equation ax^(2) + 2bx + c = 0 are alpha and beta and those of cx^(2) + 2bx + a = 0 are gamma and delta

If x^(2)+px+q=0 has the roots alpha" and "beta , then the value of (alpha-beta)^(2) is equal to

If the roots of the quadratic equation ax^(2)+bx-b=0 , where a , b in R such that a*b gt 0 , are alpha and beta , then the value of log_(|(beta-1)|)|(alpha-1)| is

If alpha and beta are the roots of ar ax^(2) + bx + c = 0 from the equation where roots are (1)/(alpha) and (1)/(beta)

CENGAGE-THEORY OF EQUATIONS-Exercise (Multiple)
  1. If (x^(2) + 5)/(2) = x - 2 cos (m + nx) has at least one real root, ...

    Text Solution

    |

  2. Let three quadratic equations ax^(2) - 2bx + c = 0, bx^(2) - 2 cx + a...

    Text Solution

    |

  3. For the quadratic equation x^2+2(a+1)x+9a-5=0, which of the following ...

    Text Solution

    |

  4. If a ,b ,c in Ra n da b c<0 , then equation b c x^2+2(b+c-a)x+a=0h a ...

    Text Solution

    |

  5. The graph of the quadratic trinomial u=a x^2+b x+c has its vertex at (...

    Text Solution

    |

  6. Let a ,b ,c in Q^+ satisfying a > b > cdot Which of the following sta...

    Text Solution

    |

  7. Let f(X) = ax^(2) + bx + c . Consider the following diagram .

    Text Solution

    |

  8. Graph of y = ax^(2) + bx + c is as shown in the figure . If PQ= 9, ...

    Text Solution

    |

  9. ax^2 + bx + c = 0(a > 0), has two roots alpha and beta such alpha < -2...

    Text Solution

    |

  10. If the equation ax^(2) + bx + c = 0, a,b, c, in R have non -real ro...

    Text Solution

    |

  11. If cos x - y^(2) - sqrt(y - x ^(2) - 1 )ge 0 , then

    Text Solution

    |

  12. If a x^2+(b-c)x+a-b-c=0 has unequal real roots for all c in R ,t h e ...

    Text Solution

    |

  13. If (x^2+a x+3)//(x^2+x+a) takes all real values for possible real valu...

    Text Solution

    |

  14. If the range of function f(x) = (x + 1)/(k+x^(2)) contains the inter...

    Text Solution

    |

  15. Consider equation (x - sin alpha) (x-cos alpha) - 2 = 0 . Which of the...

    Text Solution

    |

  16. If the roots of the equation, x^3 + px^2+qx-1 = 0 form an increasing G...

    Text Solution

    |

  17. Consider a quadratic equation ax^2 + bx + c = 0 having roots alpha, b...

    Text Solution

    |

  18. The equaiton ((x)/(x+1))^(2) + ((x)/(x-1))^(2) = a(a-1) has

    Text Solution

    |

  19. lf the quadratic equations x^2+bx+c=0 and bx^2+cx+1=0 have a common r...

    Text Solution

    |

  20. If the inequality cot^(2)x + (k +1) cot x - (k-3) < 0 is true for at ...

    Text Solution

    |