A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
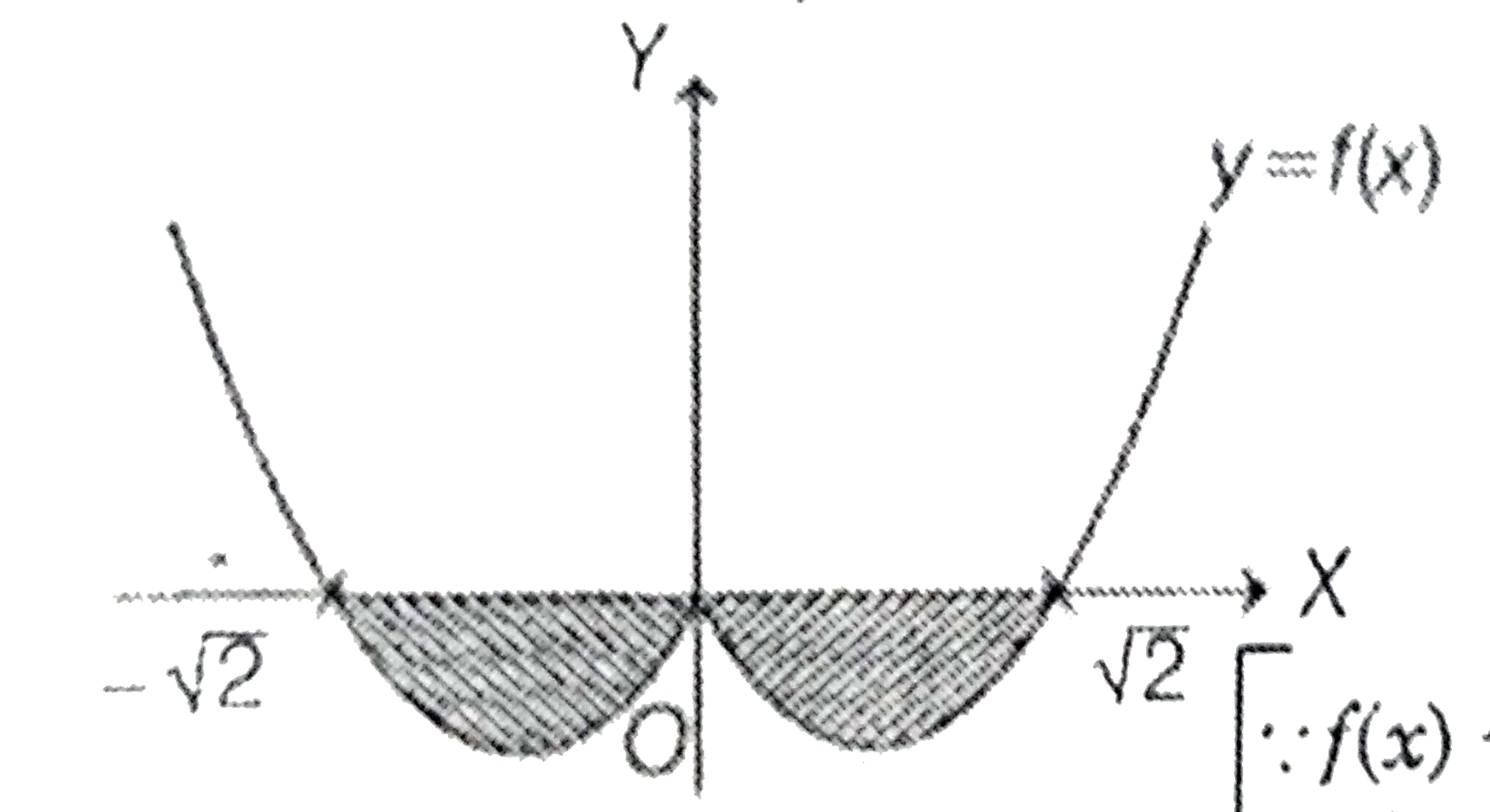
- Let i=inta^b(x^4-2x^2)dx for (a,b) which given integration is minimum ...
Text Solution
|
- Let I=inta^b (x^4−2x^2)dx for (a,b) which given integration is minimum...
Text Solution
|
- Let I=inta^b (x^4−2x^2)dx for (a,b) which given integration is minimum...
Text Solution
|
- Let I=inta^b (x^4−2x^2)dx for (a,b) which given integration is minimum...
Text Solution
|
- If U=[((1)/(sqrt2),(-1)/(sqrt2)),((1)/(sqrt2),(1)/(sqrt2))], then U^(-...
Text Solution
|
- The equation of tangent to the curve y=2 sinx at x=pi/4 is: a)y-sqrt2=...
Text Solution
|
- The equation of normal to the curve y=2cosx at x=pi/4 is: a)y-sqrt2=2...
Text Solution
|
- यदि a= (sqrt3+ sqrt2)/(sqrt3-sqrt2), b= (sqrt3-sqrt2)/(sqrt3+ sqrt2) त...
Text Solution
|
- If int[sin^2x]/[1+sin^2x] dx =x-ktan^-1(M tanx) then: a. M=1/sqrt2 b....
Text Solution
|