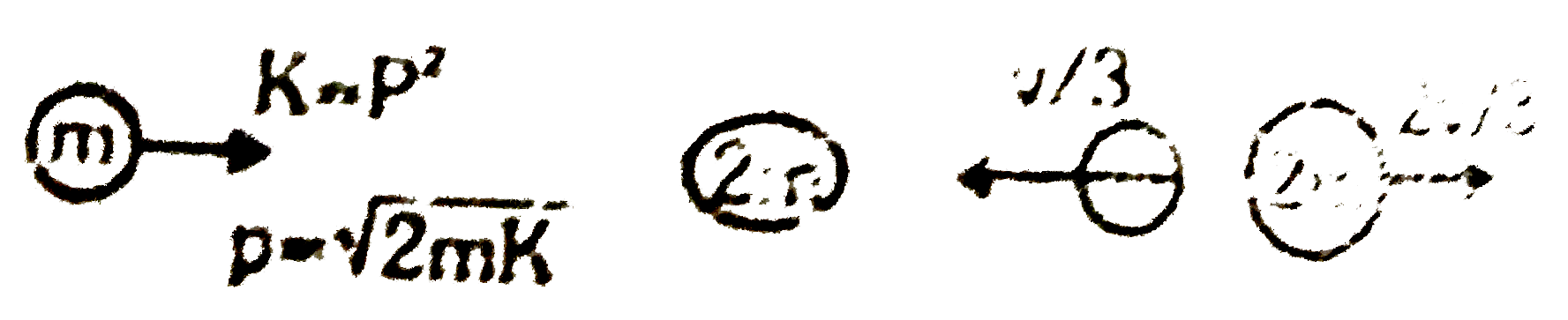Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CENTRE OF MASS
ALLEN |Exercise EXERCISE-IV A|32 VideosCENTRE OF MASS
ALLEN |Exercise EXERCISE-IV B|14 VideosCENTRE OF MASS
ALLEN |Exercise EXERCISE-II|43 VideosBASIC MATHEMATICS USED IN PHYSICS &VECTORS
ALLEN |Exercise EXERCISE-IV ASSERTION & REASON|11 VideosELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN |Exercise Exercise 5 B (Integer Type Questions)|3 Videos
Similar Questions
Explore conceptually related problems
ALLEN -CENTRE OF MASS-EXERCISE-III
- A particle of mass m, kinetic energy K and momentum p collision head o...
Text Solution
|
- Two balls of mass m and 2 m each have momentum 2p and p in the directi...
Text Solution
|
- A particle of mass 1 kg has velocity vec(v)(1) = (2t)hat(i) and anothe...
Text Solution
|
- Two blocks A and B of mass m and 2m respectively are connected by a ma...
Text Solution
|
- In each situation of column-I, a system involving two bodies is given....
Text Solution
|
- If net force on a system of particles is zero. Then {:(,"Column I",,...
Text Solution
|
- {:(,"Column I",,"Column II",),((A),"Elastic collision",(p),KE " is con...
Text Solution
|
- Assertion : In case of bullet fired from gun, the ratio of kinetic e...
Text Solution
|
- Statement -1 : When a girl jumps from a boat, the boat slightly moves ...
Text Solution
|
- Statement I: In a two-body collision, the momenta of the particles are...
Text Solution
|
- Statement-1 : The centre of mass and centre of gravity of a body are t...
Text Solution
|
- Statement-1 : A particle of mass m strikes a smooth wedge of mass M as...
Text Solution
|
- Statement-1 : The coefficient of restitution is less than one for all ...
Text Solution
|
- Statement I: No external force acts on a system of two spheres which u...
Text Solution
|
- Statement I: If a sphere of mass mmoving with speed u undergoes a perf...
Text Solution
|
- Statement I: If a ball projected up obliquely from the ground breaks u...
Text Solution
|
- Comprehension # 1 If net force on a system in a particular direction...
Text Solution
|
- Comprehension # 1 If net force on a system in a particular direction...
Text Solution
|
- Comprehension # 1 If net force on a system in a particular direction...
Text Solution
|
- Comprehension # 1 If net force on a system in a particular direction...
Text Solution
|