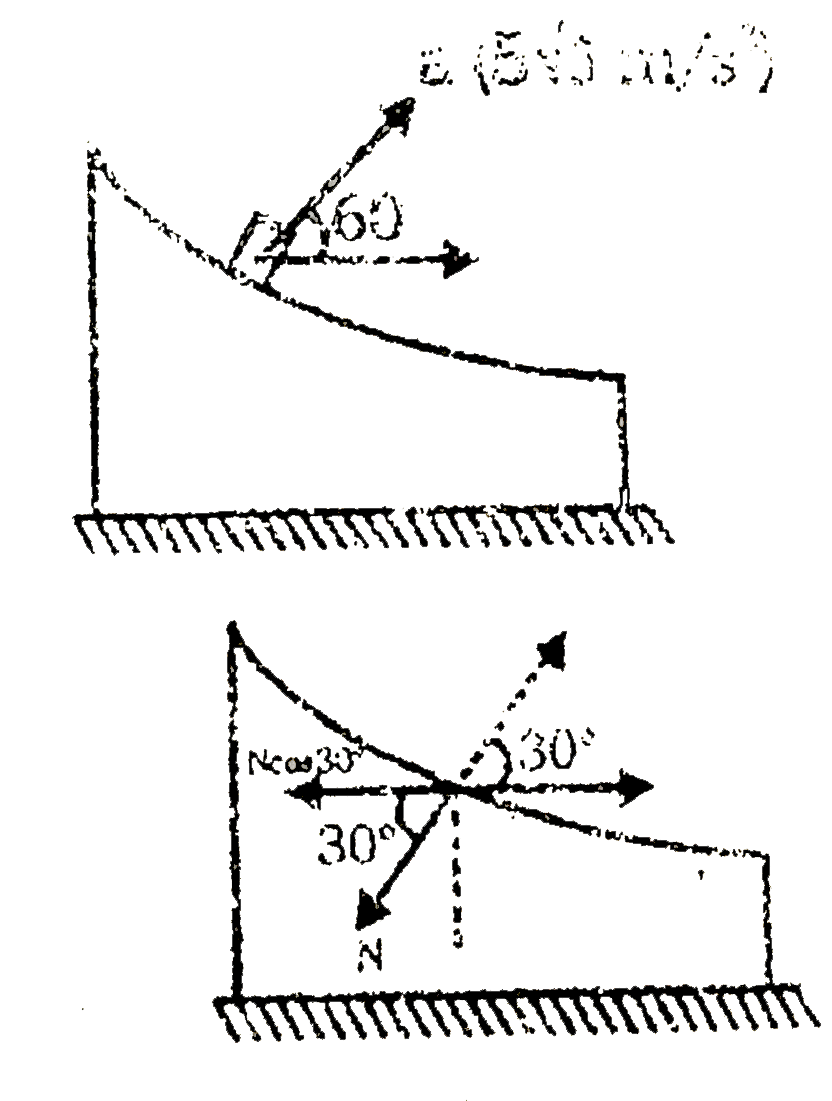A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CENTRE OF MASS
ALLEN |Exercise EXERCISE-IV A|32 VideosView PlaylistCENTRE OF MASS
ALLEN |Exercise EXERCISE-IV B|14 VideosView PlaylistCENTRE OF MASS
ALLEN |Exercise EXERCISE-II|43 VideosView PlaylistBASIC MATHEMATICS USED IN PHYSICS &VECTORS
ALLEN |Exercise EXERCISE-IV ASSERTION & REASON|11 VideosView PlaylistELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN |Exercise Exercise 5 B (Integer Type Questions)|3 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
ALLEN -CENTRE OF MASS-EXERCISE-III
- Comprehension # 1 If net force on a system in a particular direction...
02:44
|
Play - Comprehension # 1 If net force on a system in a particular direction...
03:26
|
Play - Comprehension # 1 If net force on a system in a particular direction...
02:22
|
Playing Now - Comprehension # 1 If net force on a system in a particular direction...
02:15
|
Play - Comprehension # 2 When two bodies collide normally they exert equal ...
03:22
|
Play - Comprehension # 2 When two bodies collide normally they exert equal ...
03:27
|
Play - A ball collides at B with velocity 10m//s at 30^(@) with vertical. The...
02:58
|
Play - Comprehension # 4 When the mass of a sytem is variable, a thrust for...
Text Solution
|
Play - Comprehension # 4 When the mass of a sytem is variable, a thrust for...
Text Solution
|
Play - Comprehension # 5 One particle of mass 1 kg is moving along positive...
03:37
|
Play - Comprehension # 5 One particle of mass 1 kg is moving along positive...
03:50
|
Play - Comprehension # 5 One particle of mass 1 kg is moving along positive...
02:57
|
Play - Comprehension # 6 A 1 kg block is given a velocity of 15 m//s toward...
02:33
|
Play - Comprehension # 6 A 1 kg block is given a velocity of 15 m//s toward...
02:18
|
Play - Comprehension # 6 A 1 kg block is given a velocity of 15 m//s toward...
02:16
|
Play - Two blocks of equal mass m are connected by an unstretched spring and ...
01:29
|
Play - Two blocks of equal mass m are connected by an unstretched spring and ...
01:53
|
Play - Two blocks of equal mass m are connected by an unstretched spring and ...
01:39
|
Play - Comprehension # 8 An initially stationary box on a frectionless floo...
02:28
|
Play - An initially stationary box on a frectionless floor explodes into two ...
02:48
|
Play