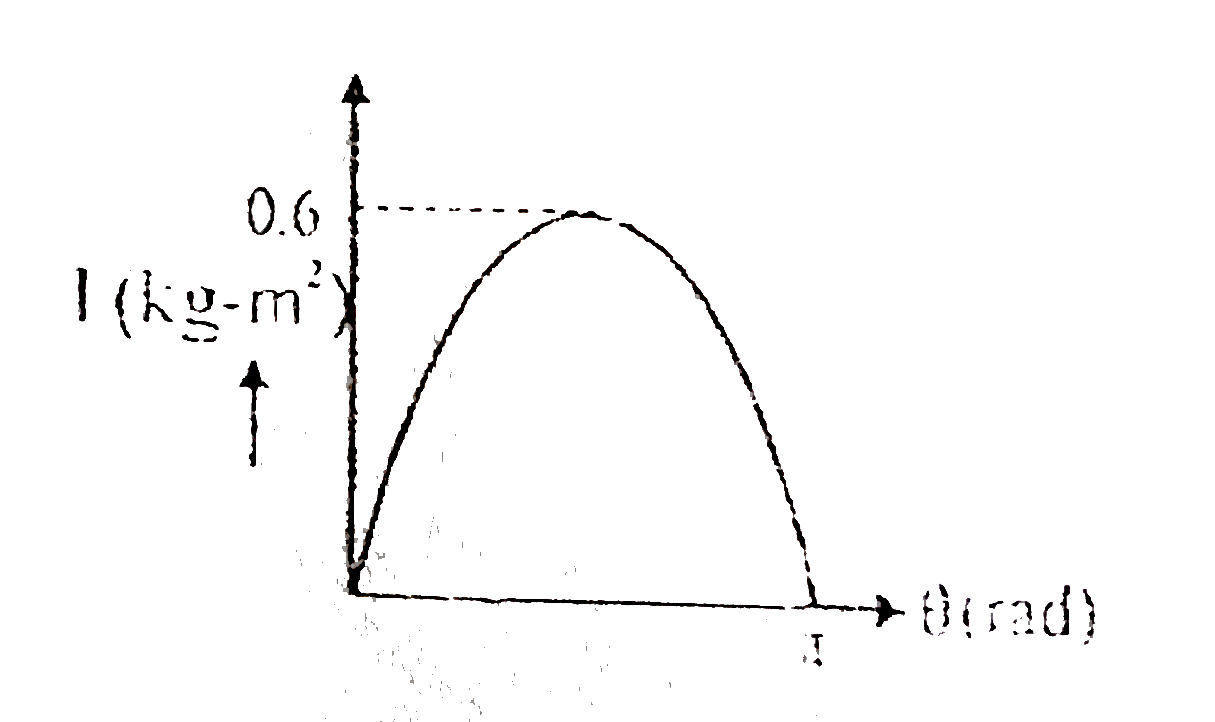A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
TEST PAPER
ALLEN |Exercise PHYSICS|4 VideosView PlaylistTEST PAPER
ALLEN |Exercise PHYSICS|4 VideosView PlaylistSIMPLE HARMONIC MOTION
ALLEN |Exercise Example|1 VideosView PlaylistTEST PAPER 1
ALLEN |Exercise PHYSICS|11 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
ALLEN -TEST PAPER-Exercise (Physics)
- The figure shows an isosceles triangle plate of mass M and base L. T...
01:52
|
Play - A pulley is connected to the ceiling of an elevator by a massless rod....
01:43
|
Play - Figure shows the variation of the moment of inertia of a uniform rod, ...
01:15
|
Playing Now - Four rigid bodies, each with the same mass and radius, are spinning fr...
03:59
|
Play - Particles of masses m,2m,3m,…….nm grams are placed on the same line at...
02:40
|
Play - A disc of the radius R is confined to roll without slipping at A and B...
01:50
|
Play - A solid cylinder C and a hollow pipe P of same diameter are in contact...
05:48
|
Play - A ball of mass m collides horizontally with a stationary wedge on a ro...
02:17
|
Play - Shown in the figure is a system of three particles of mass 1 kg, 2 kg ...
03:18
|
Play - A particle of mass m moving with velocity v makes head-on elastic coll...
02:33
|
Play - which of the following forces can never, under any circumstances, does...
01:04
|
Play - A body (intially at rest is falling under gravity. When it loses a gra...
01:10
|
Play - Position time graph of a particle of mass 2 kg is shown in figrure. To...
03:55
|
Play - A block of mass m lies on a horizontal frictionless surface and is att...
05:49
|
Play - Block A of mass 1 kg is placed on the rough surface of block B of mass...
04:47
|
Play - One end of a light spring of natural length 4m and spring constant 170...
02:40
|
Play - A particle of mass 1 kg moves in a circular path of radius 1 m such th...
02:01
|
Play - Infinite rods of uniform mass density and length L,L/2,L/4….. Are plac...
02:36
|
Play - A semicircular lamina of mass m and radius r and centre C. Its center ...
01:18
|
Play - The position vector of a particle in a circular motion about the origi...
01:53
|
Play