Home
Class 11
PHYSICS
A particle is moving in a circular orbit...

A particle is moving in a circular orbit when a constant tangential acceleration. After `2s` from the beginning of motion, angle between the total acceleration vector and the radius E becomes `45^(@)`. What is the angular acceleration of the particle?

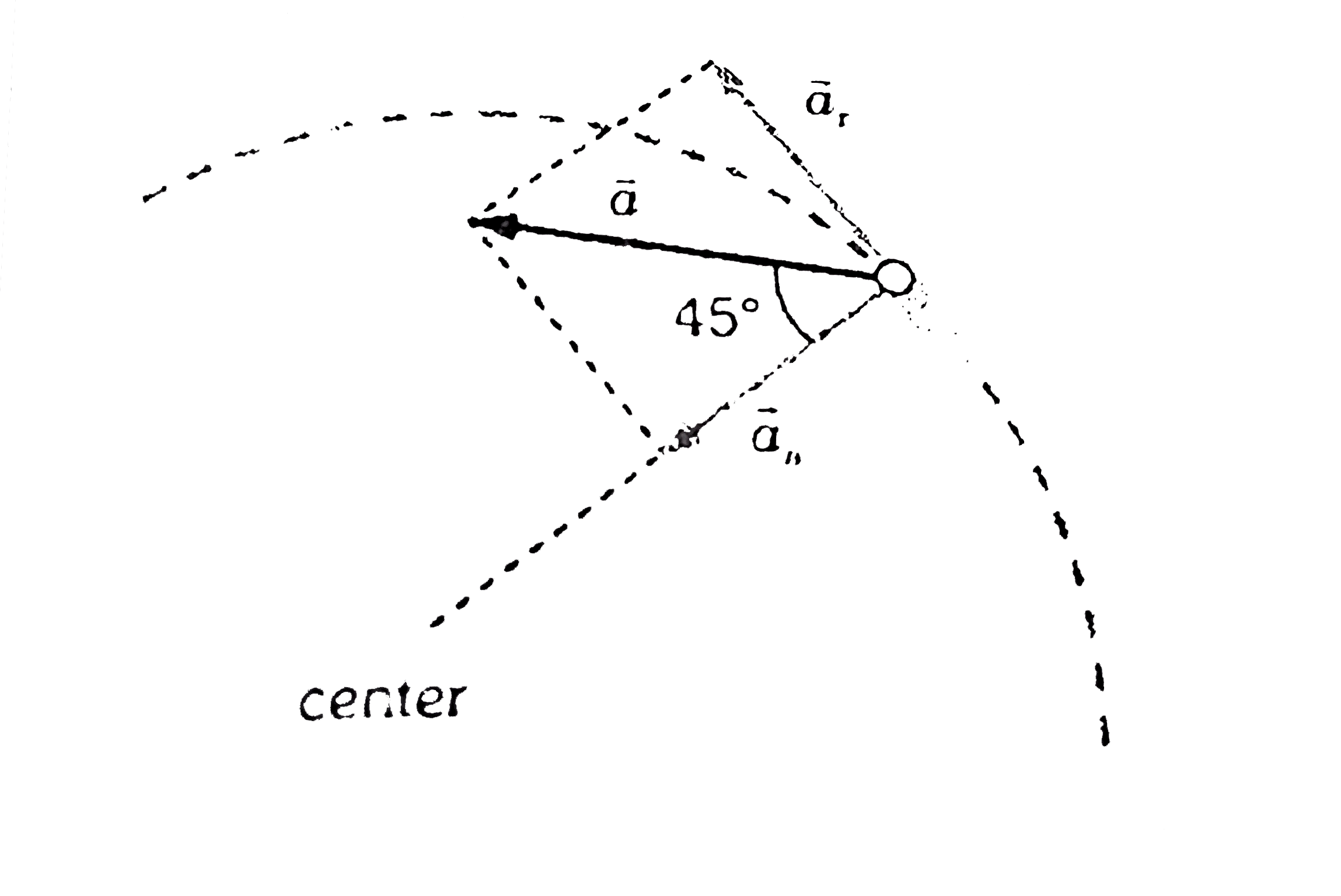
Text Solution

Verified by Experts

In the adjoining figure are shown the total acceleration vector `vec(a)` and its components the tangential accelerations `vec(a)_(tau)` and normal acceleration `vec(a)_(n)` are shown. These two components are always mutually perpendicular to each other and act along the tangent to the circle and radius respectively. Therefore, if the total acceleration vector makes an angle of `45^(@)` with the radius, both the tangential and the normal components must be equal in magnitudr.
Now from equation and, we have
`a_(tau)=a_(n) rarr alpha R=omega^(2)R rArr alpha=omega^(2)` ...(i)
Since angular acceleration is uniform, form equation, we have `omega=omega_(o)+alphat`
Substituting `omega_(0)=0` and `t=2 s`, we have `omega=2alpha` ...(ii)
From equation (i) and (ii), we have `alpha=0.25 rad//s^(2)`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • KINEMATICS

    ALLEN |Exercise EXERCISE-01|55 Videos

  • KINEMATICS

    ALLEN |Exercise EXERCISE-02|57 Videos

  • ERROR AND MEASUREMENT

    ALLEN |Exercise Part-2(Exercise-2)(B)|22 Videos

  • KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)

    ALLEN |Exercise BEGINNER S BOX-7|8 Videos

Similar Questions

Explore conceptually related problems

A particle is moving in a circular orbit with a constant tangential acceleration. After a certain time t has elapsed after the beginning of motion, the between the total acceleration a and the direction along the radius r becomes equal to 45^(@) . What is the angular acceleration of the particle.

A point mass moves along a circle of radius R with a constant angular acceleration alpha . How much time is needed after motion begins for the radial acceleration of the point mass to be equal to its tangential acceleration ?

Knowledge Check

  • A particle of mass 10 g moves along a circle of radius 6.4 cm with constant tangential acceleration. What is the magnitude of this acceleration if the kinetic energy of the particle becomes equal 8xx10^(-4)J by the end of the second revolution after the beginning of the motion?

    A
    `0.15m//s^(2)`
    B
    `0.18m//s^(2)`
    C
    `0.2m//s^(2)`
    D
    `0.1m//s^(2)`

    • Similar Questions

    Explore conceptually related problems

    Assertion:- A particle is moving in a circle with constant tangential acceleration such that its speed v is increasing. Angle made by resultant acceleration of the particle with tangential acceleration increases with time. Reason:- Tangential acceleration =|(dvecv)/(dt)| and centripetal acceleration =(v^(2))/(R)

    A particles is moving on circular path of radius R with constant angular velocity omega . Its centripetal acceleration will be …... .

    A particle is moving with a velocity of vec(v)=(3hat(i)+4that(j))m//s . Find the ratio of tangential acceleration to that of total acceleration at t=1sec

    A particle is moving on a circular path such that at any instant its position vector, linear velocity. Angular velocity, angular acceleration with respect to centre are vec(r),vec(v),vec(w),vec(alpha) respectively. Net acceleration of the particle is :-

    Will the tangential acceleration of a particle moving on a fixed circle always be zero? When it is zero?

    A particle is moving on a circular path of radius 1.5 m at a constant angular acceleration of 2 rad//s^(2) . At the instant t=0 , angular speed is 60//pi rpm. What are its angular speed, angular displacement, linear velocity, tangential acceleration and normal acceleration and normal acceleration at the instant t=2 s .

    A particle is moving along a circular path ofradius R in such a way that at any instant magnitude of radial acceleration & tangential acceleration are equal. 1f at t = 0 velocity of particle is V_(0) . Find the speed of the particle after time t=(R )//(2V_(0))

    Home
    Profile