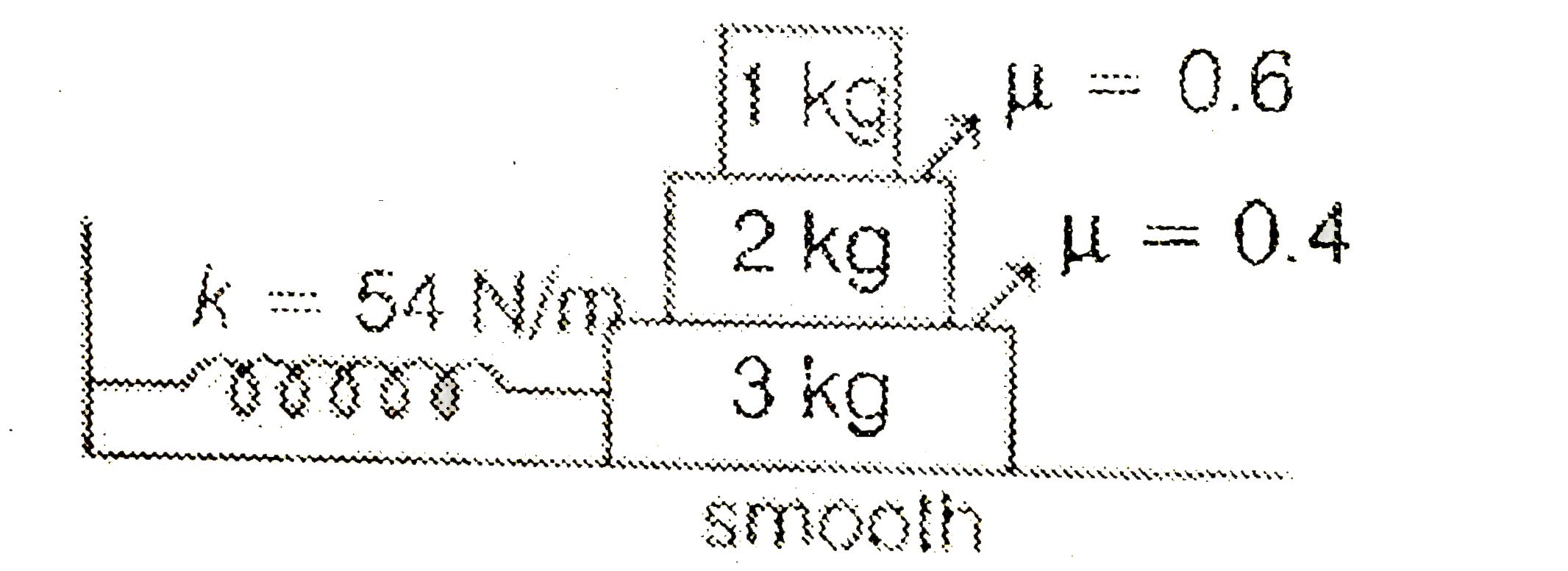Home
Class 12
PHYSICS
Passage IV) Angular frequency in SHM is ...

Passage IV) Angular frequency in SHM is given by `omega=sqrt(k/m)`. Maximum acceleration in SHM is `omega^(2)` A and maximum value of friction between two bodies in contact is `muN`, where N is the normal reaction between the bodies.

In the figure shown, what can be the maximum amplitude of the system so that there is no slipping between any of hte blocks?

A

`2/7 m`

B

`3/4 m`

C

`4/9 m`

D

`10/3 m`

Text Solution

Verified by Experts

The correct Answer is:
C
Max. acceleration of `1kg`
`= ((0.6)(1)(10))/(1) = 6ms^(2)`
Max. acceleration of 2kg
`= ((0.4)(3)(10))/(3) = 4ms^(-2)`
Therefore maximum acceleration of system can be `4 m//s^(2)`
`rArr omega^(2)A =4 rArr A = (4)/(omega^(2)) = (4)/((k//m)) = (4)/(54//6) = 4/9m`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • SIMPLE HARMONIC MOTION

    ALLEN |Exercise Comprehension Base Questions (2)|2 Videos

  • SIMPLE HARMONIC MOTION

    ALLEN |Exercise Comprehension Base Questions (3)|2 Videos

  • SIMPLE HARMONIC MOTION

    ALLEN |Exercise Asseration & Reason|7 Videos

  • RACE

    ALLEN |Exercise Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)|25 Videos

  • TEST PAPER

    ALLEN |Exercise PHYSICS|4 Videos

Similar Questions

Explore conceptually related problems

Passage IV) Angular frequency in SHM is given by omega=sqrt(k/m) . Maximum acceleration in SHM is omega^(2) A and maximum value of friction between two bodies in contact is muN , where N is the normal reaction between the bodies. Now the value of k, the force constant is increased, then the maximum amplitude calcualted in above question will

The friction coefficient between the board and the floor shown in figure is mu Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

Knowledge Check

  • The coefficient of static friction mu s, between block A of mass 2 kg and the table as shown in the figure is 0.2. What would be the maximum mass value of block B, so that two blocks do not move ? The string and the pully are assumed to be smooth and massless.

    A
    4.0 kg
    B
    0.2 kg
    C
    0.4 kg
    D
    2.0 kg

    • Similar Questions

    Explore conceptually related problems

    The system shown in the figure is in equilibrium The maximum value of W, so that the maximum value of static frictional force on 100kg. body is 450N, will be:

    The coefficient of static friction mu s, between block A of mass 2 kg and the table as shown in the figure is 0.2. What would be the maximum mass value of block B, so that two blocks do not move ? The string and the pully are assumed to be smooth and massless.

    In the figure given, the system is in equilibrium. What is the maximum value that W can have if the friction force on the 40N block can not exceed 12.0N?

    Two bodies performing S.H.M. have same amplitude and frequency. Their phases at a certain instant are as shown in the figure. The phase difference between them is

    The coefficient of static friction, mu_(s) between block A of mass 2 kg and the table as shown in the figure is 0.2. What would be the maximum mass value of block B so that the two blocks do not move? The string and the pulley are assumed to be smooth and massless. (g=10m//s^(2))

    Two particle P and Q describe S.H.M. of same amplitude a same frequency f along the same straight line .The maximum distance between the two particles is asqrt(2) The phase difference between the two particle is

    Two blocks of mass m_(1)=10kg and m_(2)=5kg connected to each other by a massless inextensible string of length 0.3m are placed along a diameter of the turntable. The coefficient of friction between the table and m_(1) is 0.5 while there is no friction between m_(2) and the table. the table is rotating with an angular velocity of 10rad//s . about a vertical axis passing through its center O . the masses are placed along the diameter of the table on either side of the center O such that the mass m_(1) is at a distance of 0.124m from O . the masses are observed to be at a rest with respect to an observed on the tuntable (g=9.8m//s^(2)) . (a) Calculate the friction on m_(1) (b) What should be the minimum angular speed of the turntable so that the masses will slip from this position? (c ) How should the masses be placed with the string remaining taut so that there is no friction on m_(1) .

    Home
    Profile