Home
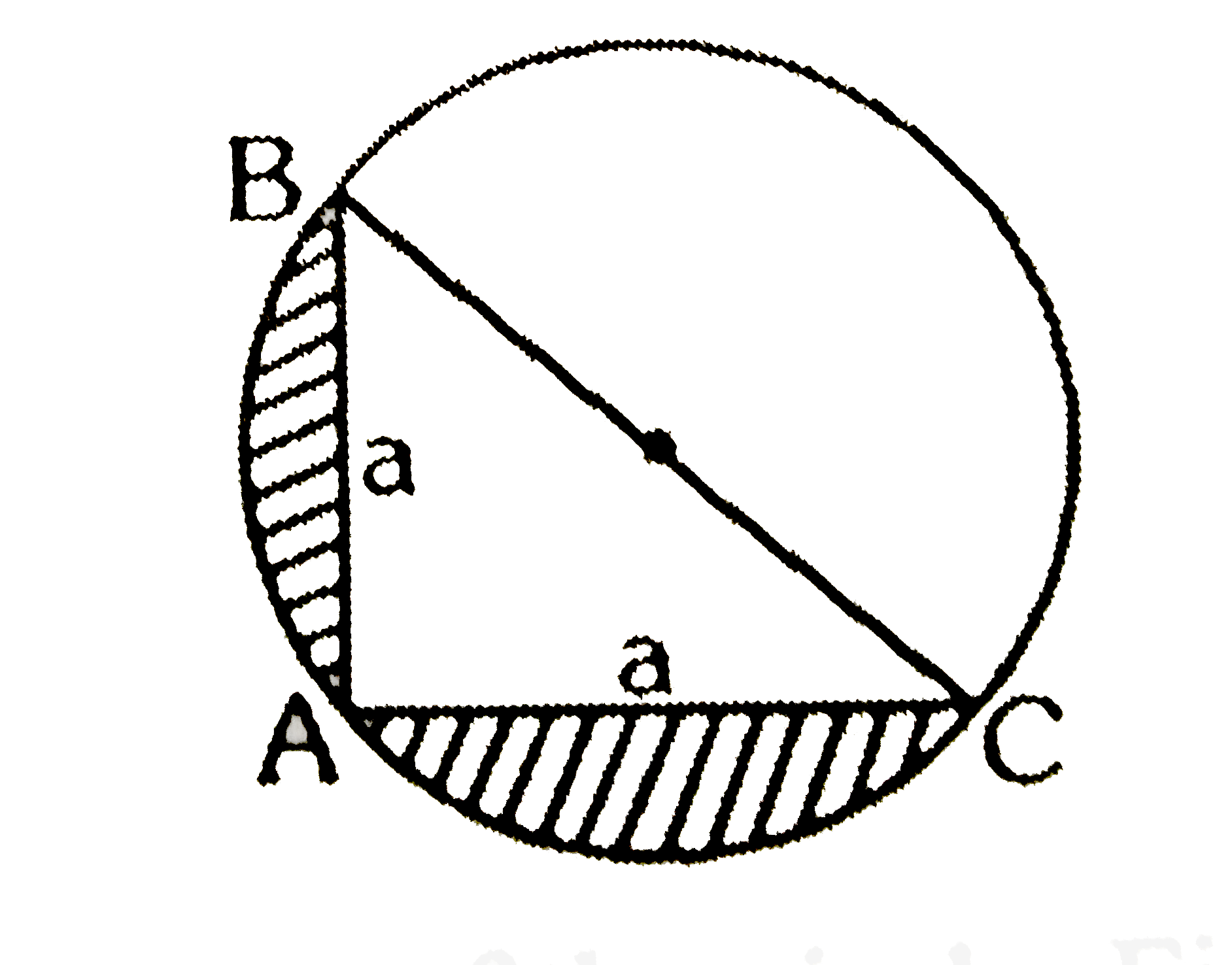
Class 12
MATHS
If BC passes through centre of the circl...

If BC passes through centre of the circle, then the area of the shaded region in the given figure is:

A

`(a^(2))/(2)(3-pi)`

B

`a^(2)((pi)/(2)-1)`

C

`2a^(2)(pi-1)`

D

`(a^(2))/(2)((pi)/(2)-1)`

Text Solution

Verified by Experts

The correct Answer is:
D
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

Similar Questions

Explore conceptually related problems

In the given figure, find the area of the shaded region. (Use pi = 3.14 )

In the given figure, ABCD is a trapezium with AB||DC , AB = 18 cm, DC = 32 cm and distance between AB and DC = 12 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.

Knowledge Check

  • The shaded region in the given figure is a graph of ……………

    A
    `4x-2y le 3`
    B
    `4x-2y le -3`
    C
    `2x-4y ge 3`
    D
    `2x-4y le -3`

    • Similar Questions

    Explore conceptually related problems

    Find the area of the shaded region in the given figure, where ABCD is a square of side 14 cm.

    In the given figure, AB = 36 cm and M is the midpoint of AB. Semicircles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of shaded region. [Hint : Take O as the centre of semicircle on diameter AM. Take the radius of the circle with centre C as r. Then , OC = (9 + r)cm, OM = 9 cm and CM = (18-r) cm. Now, use Pythagoras theorem and find r = 6 cm.]

    In the given figure AB is a semicircle with centre O. Find the perimeter and the area of the shaded region correct upto one decimal place. Here, AC = 12 cm and BC = 16 cm. (Use pi = 3.14 )

    In the following figure, if PQ = R (P is the centre of the bigger circle) and the shaded area is equal to A, then the radius of the inner circle is equal to -

    The differential equation of circles passing through the points of intersection of unit circle with centre at the origin and the line bisecting the first quadrant, is

    The diameter of a coin is 1 cm. If four such coins are palced on a table as shown in the figure such that the rim of each touches that of the other two, find the area of the shaded region. (Use pi = 3.1416 )

    The area of an equilateral triangle ABC is 17320.5 cm^(2) . With each vertex of the triangle as centre, a circle is drawn with radius to half the length of the side of the triangle (see the given figure). Find the area of the shaded region. (Use pi = 3.14 and sqrt(3) = 1.73205 )

    Home
    Profile