Home
Class 12
PHYSICS
Figure shows three vectors veca,vecb and...

Figure shows three vectors `veca,vecb` and `vecc`. If `bar(RQ)=2bar(PR)`, which of the following relation is correct :-

A

`2veca+vecc=3vecb`

B

`veca+3vecc=2vecb`

C

`3veca+vecc=2vecb`

D

`veca+2vecc=3vecb`

Text Solution

Verified by Experts

The correct Answer is:
D
Promotional Banner

Topper's Solved these Questions

  • RACE

    ALLEN |Exercise Basic Maths (Units, Dimensions & Measurements)|37 Videos

  • RACE

    ALLEN |Exercise Basic Maths (KINEMATICS)|63 Videos

  • RACE

    ALLEN |Exercise Basic Maths (Co-ordinate & Algebra)|40 Videos

  • NEWTONS LAWS OF MOTION

    ALLEN |Exercise EXERCISE-III|28 Videos

  • SIMPLE HARMONIC MOTION

    ALLEN |Exercise Example|1 Videos

Similar Questions

Explore conceptually related problems

Figure shows three vectors vec(a), vec(b) and vec(c) , where R is the midpoint of PQ. Then which of the following relations is correct?

Given three vectors veca, vecb and vecc are non-zero and non-coplanar vectors. Then which of the following are coplanar.

Two vectors vecA and vecB are such that vecA+vecB=vecC and A^(2)+B^(2)=C^(2) . Which of the following statements, is correct:-

Column-I show vector diagram relating three vectors veca, vecb " and " vecc . Match the vector equation in column -II, with vector diagram in column-I:

Three vectors veca,vecb and vecc satisfy the relation veca.vecb=0 and veca.vecc=0 . The vector veca is parallel to

In vector diagram shown in figure where (vecR) is the resultant of vectors (vecA) and (vecB) . If R= (B)/(sqrt2) , then value of angle theta is :

Assertion: If three vectors vecA,vecB and vecC satisfy the relation vecA.vecB=0 & vecA.veC=0 then the vector vecA may be parallel to

Statement 1 : Let A(veca), B(vecb) and C(vecc) be three points such that veca = 2hati +hatk , vecb = 3hati -hatj +3hatk and vecc =-hati +7hatj -5hatk . Then OABC is tetrahedron. Statement 2 : Let A(veca) , B(vecb) and C(vecc) be three points such that vectors veca, vecb and vecc are non-coplanar. Then OABC is a tetrahedron, where O is the origin.

If veca and vecb are two non- zero collinear vectors then …… is correct .

Theree coplanar vectors vecA,vecB and vecC have magnitudes 4.3 and 2 respectively. If the angle between any two vectors is 120^(@) then which of the following vector may be equal to (3vecA)/(4)+(vecB)/(3)+(vecC)/(2)

ALLEN -RACE-Basic Maths (VECTORS)
  1. Which of the following group of forces cannot produce zero resultan?

    Text Solution

    |

  2. If costheta = 5/3 then what is the value of cos(theta/2)?

    Text Solution

    |

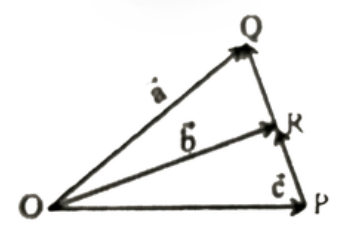
  3. Figure shows three vectors veca,vecb and vecc. If bar(RQ)=2bar(PR), wh...

    Text Solution

    |

  4. 100 coplanar forces each equal to 10 n act on a body. Each force makes...

    Text Solution

    |

  5. With respect to a rectangular cartesian coordinate system, three vecto...

    Text Solution

    |

  6. There are two force vectors, one of 5N and other of 12N. At what angle...

    Text Solution

    |

  7. Two equal forces are acting at a point with an angle of 60^(@) between...

    Text Solution

    |

  8. Two forces 3 N and 2 N are at an angle theta such that the resultant i...

    Text Solution

    |

  9. The resultant of the vectors A and B is perpendicular to the vector A ...

    Text Solution

    |

  10. Two force F(1)" and "F(2) are acting on a body. One force is double th...

    Text Solution

    |

  11. Two vectors vecA" and "vecB have equal magnitudes. If magnitude of vec...

    Text Solution

    |

  12. The maximum and minimum resultant of two forces acting at a point are ...

    Text Solution

    |

  13. The resultant of the three vectors bar(OA),bar(OB) and bar(OC) shown i...

    Text Solution

    |

  14. If (|veca+vecb|)/(|veca-vecb|)=1, then angle between bar(a)" and "bar(...

    Text Solution

    |

  15. The magnitude of pairs of displacement vectors are give. Which pairs o...

    Text Solution

    |

  16. I started walking down a road to day-break facing the sun. After walki...

    Text Solution

    |

  17. vecA, vecB" and "vecC are three orthogonal vectors with magnitudes 3, ...

    Text Solution

    |

  18. In the shown figure what amount of force and in which direction we sho...

    Text Solution

    |

  19. Given veca+vecb=2hati," if "vecb=3hatj-hatk then find out vector veca ...

    Text Solution

    |

  20. Whtch of the following statement is true :-

    Text Solution

    |