Recommended Questions
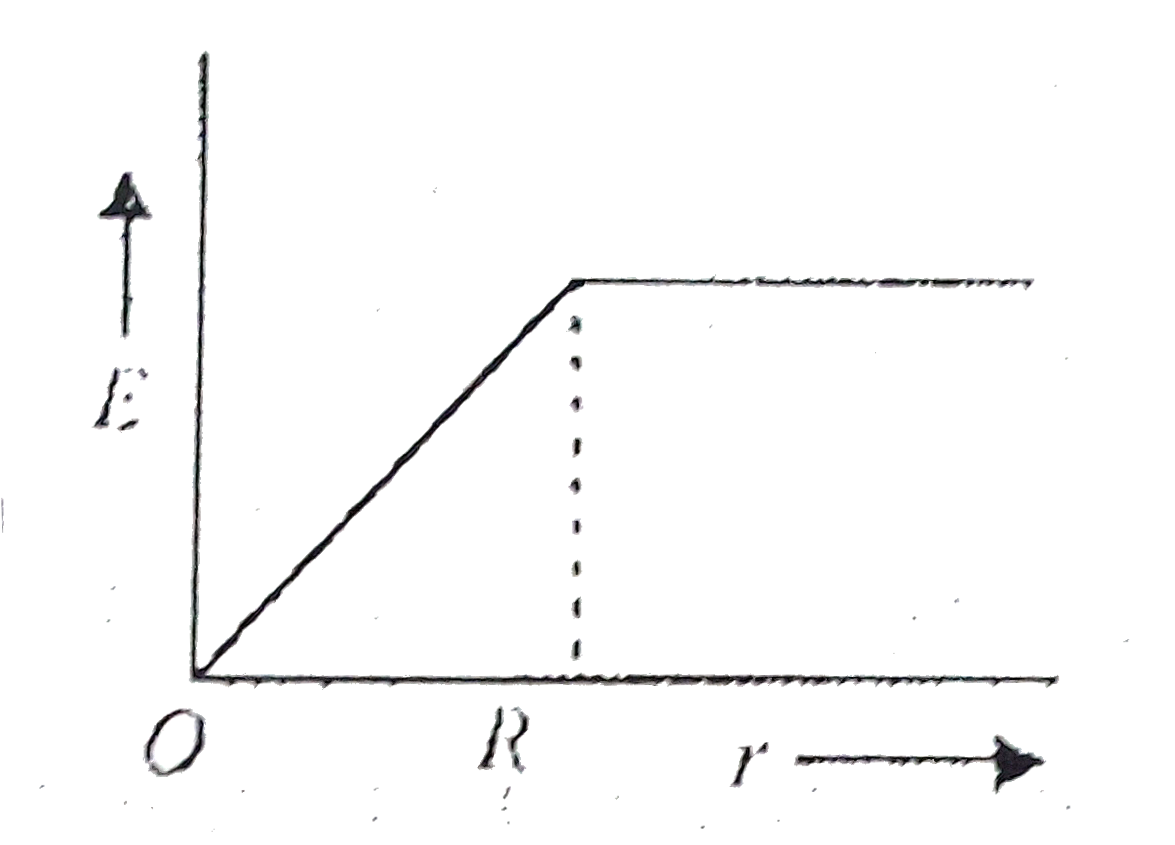
- The electric field due to uniformly charged sphere of radius R as a fu...
03:42
|
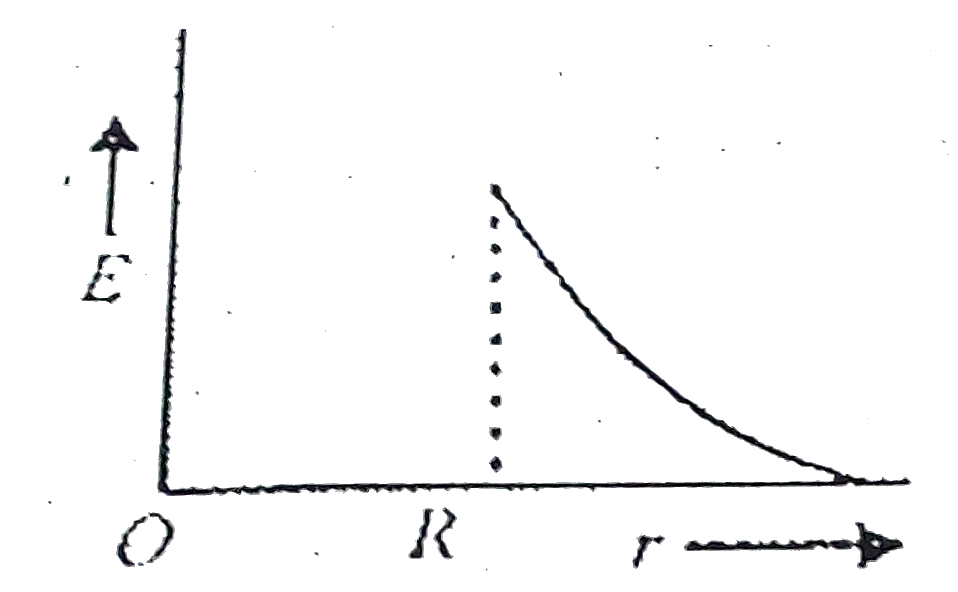
Playing Now - A non-conducting solid sphere of radius R is uniformly charged. The ma...
04:20
|
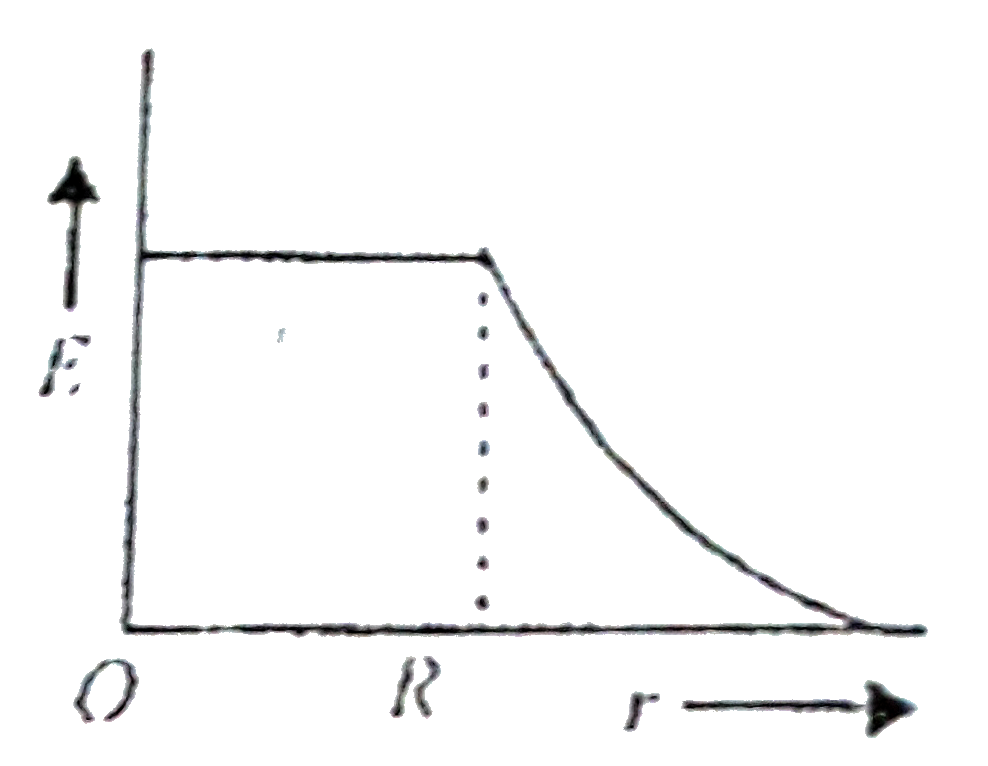
Play - A hallow metal sphere of radius R is uniformly charged. The electric f...
03:28
|
Play - The electric field due to uniformly charged sphere of radius R as a fu...
04:44
|
Play - A non-conducting solid sphere of radius R is uniformly charged. The ma...
04:20
|
Play - A non conducting solid sphere of radius R is uniformly charged. The ma...
07:30
|
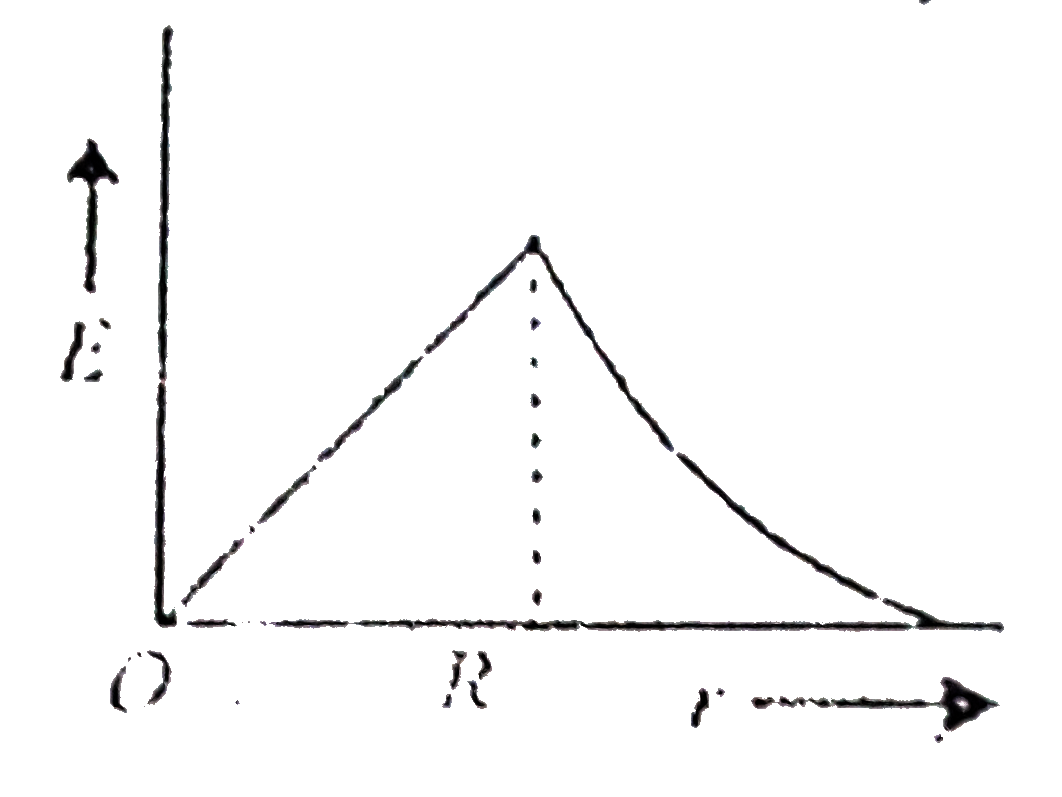
Play - A sphere of radius R, is charged uniformly with total charge Q. Then c...
04:53
|
Play - Which graph best represents the variation of electric potential as a f...
01:28
|
Play - A hollow metal sphere of radius R is uniformly charged. The electric f...
04:06
|
Play