Recommended Questions
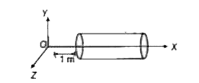
- A hollow cylindrical box of length 1 m and area of cross -section 25" ...
08:43
|
Playing Now - A cube has sides of length L = 0.300 m. It is placed with one corner a...
14:48
|
Play - A cube has sides of length L = 0.300 m. It is placed with one corner a...
14:48
|
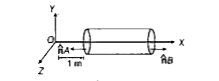
Play - A hollow cylindrical box of length 1m and area of cross section 25 cm...
05:33
|
Play - A hollow cylindrical box of length 0.5m and area of cross-section 20cm...
04:56
|
Play - A cube of side l is placed in a uniform field E, where E= E hat(i) ...
Text Solution
|
Play - Net electric flux through a sphere of radius 1 m placed in a uniform e...
03:26
|
Play - An infinite line charge is at the axis of a cylinder of length 1 m and...
04:08
|
Play - A hollow cylindrical box of length 1m area of cross-section 25 cm^(2)...
Text Solution
|
Play