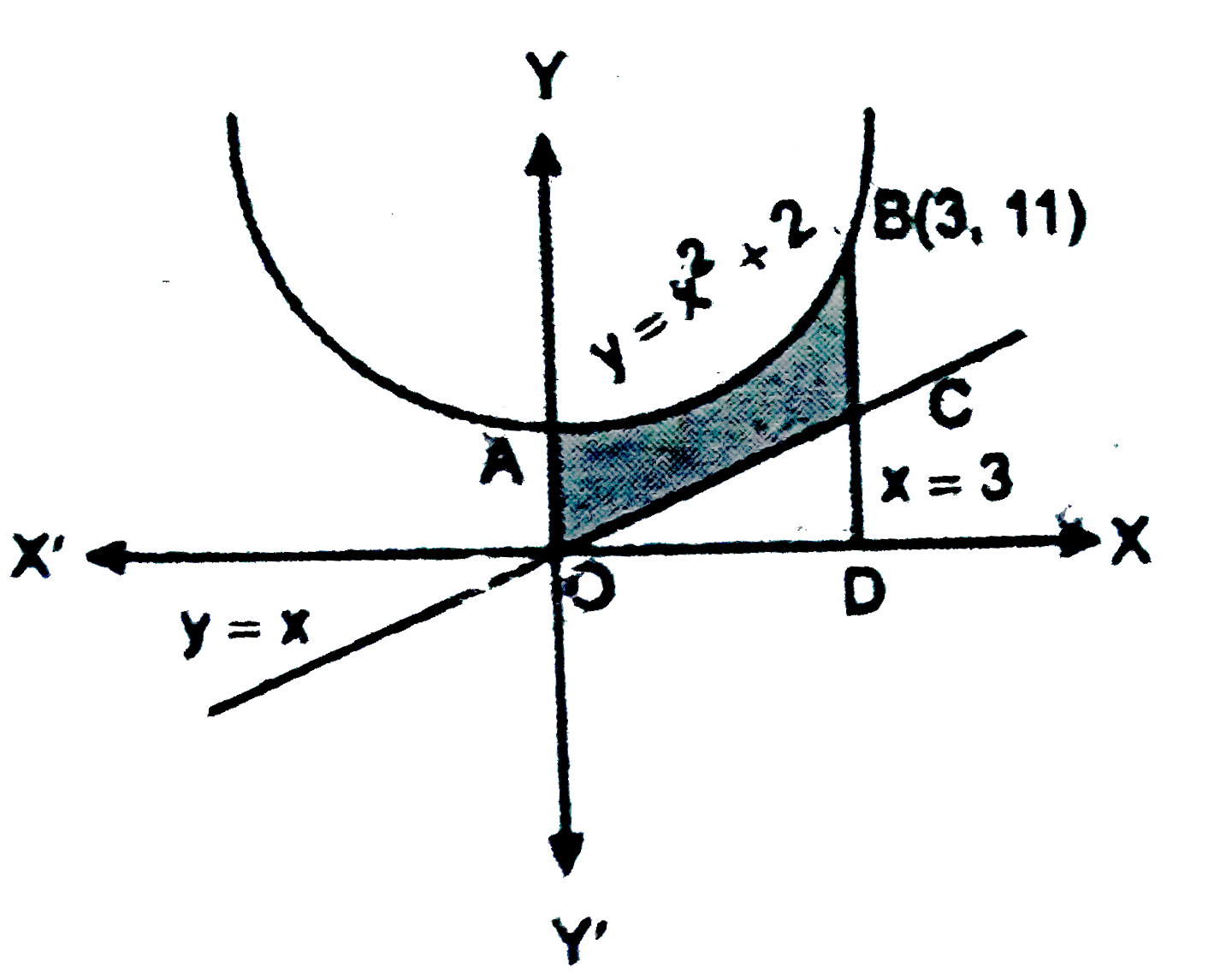Text Solution
Verified by Experts
|
Topper's Solved these Questions
APPLICATION OF DERIVATIVES
CENGAGE PUBLICATION|Exercise All Questions|674 VideosView PlaylistAPPLICATIONS OF DERIVATIVES
CENGAGE PUBLICATION|Exercise Subjective Type|2 VideosView Playlist
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-APPLICATION OF INTEGRALS-All Questions
- A curve is given by y={(sqrt(4-x^2)),0lt=x<1and sqrt((3x)),1lt=xlt=...
07:40
|
Play - Find the area enclosed by the curves x^2=y , y=x+2 and x-axis
04:52
|
Play - Find the area of the region bounded by the curves y=x^2+2, y=x ,x=0,a ...
04:29
|
Playing Now - Find the area of that part of the circle "x"^2+" y"^2=16 which is ex...
14:01
|
Play - Find the area bounded by the y-axis, y=cosx ,and y=sinx when 0lt=xlt=p...
03:25
|
Play - Find the area lying in the first quadrant and bounded by the curve y=x...
04:34
|
Play - If the area enclosed by curve y=f(x)a n dy=x^2+2 between the abscissa ...
08:42
|
Play - Plot the region in the first quadrant in which points are nearer to th...
06:40
|
Play - Find the area bounded by the curve y=sin^(-1)x and the line x=0,|y|=pi...
01:53
|
Play - Find the area of the region bounded by the limits x=0,x=pi/2,a n df(x)...
04:41
|
Play - The area bounded by y=sec^-1 x,y=cosec^-1x, and line x-1=0 is (a) log(...
08:21
|
Play - The area of the region whose boundaries are defined by the curves y=2c...
02:27
|
Play - Area bounded by the curve x y^2=a^2(a-x) and the y-axis is (pia^2)/2s ...
05:31
|
Play - The area of the closed figure bounded by x=-1,y=0,y=x^2+x+1, and the t...
05:11
|
Play - The area of the closed figure bounded by y=(x^2)/2-2x+2 and the tangen...
10:45
|
Play - The area of the closed figure bounded by x=-1,x=2,a n d y={-x^2+2,xlt...
03:51
|
Play - The area between the curve y=2x^4-x^2, the axis, and the ordinates of ...
08:35
|
Play - The area bounded by the curve a^2y=x^2(x+a) and the x-axis is (a^2)/3s...
05:42
|
Play - Find the area bounded by the curve x^(2) = 4y and the line x = 4y - 2.
06:20
|
Play - If S is the sum of cubes of possible value of c for which the area of ...
06:41
|
Play