Text Solution
Verified by Experts
|
Topper's Solved these Questions
MATHMETICAL REASONING
CENGAGE PUBLICATION|Exercise Single correct answer type|38 VideosView PlaylistMATHMETICAL REASONING
CENGAGE PUBLICATION|Exercise Archives|10 VideosView PlaylistMATHMETICAL REASONING
CENGAGE PUBLICATION|Exercise Archives|10 VideosView PlaylistLOGARITHM AND ITS PROPERTIES
CENGAGE PUBLICATION|Exercise JEE ADVANCED|1 VideosView PlaylistMATRICES
CENGAGE PUBLICATION|Exercise All Questions|509 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-MATHMETICAL REASONING-concept application
- Write down the truth table for the compound statements : (~pvvq)^^(~...
03:00
|
Play - Find the truth values of the following compound statements : (a) (pv...
14:41
|
Play - Find the truth values of (a) ~p to (q to p) " " (b) ( p to q) t...
04:54
|
Play - Find the truth values of (a) (pharr~q) harr(q to p) " " (b) (p to...
11:10
|
Play - Construct the truth table for the followings statements : (a) (p^^q)...
10:48
|
Play - Prove that the statement -~(pharr q) harr {(p^^~q) vv (~p^^q)} is a ta...
02:50
|
Play - Are the following statements equivalent : 'If the trades do not redu...
06:10
|
Play - For the statement: "If a quadrilateral is a rectangle , then it has tw...
02:32
|
Play - Show that (p^^q)vv(~p)vv(p^^~q) is a tautology
05:05
|
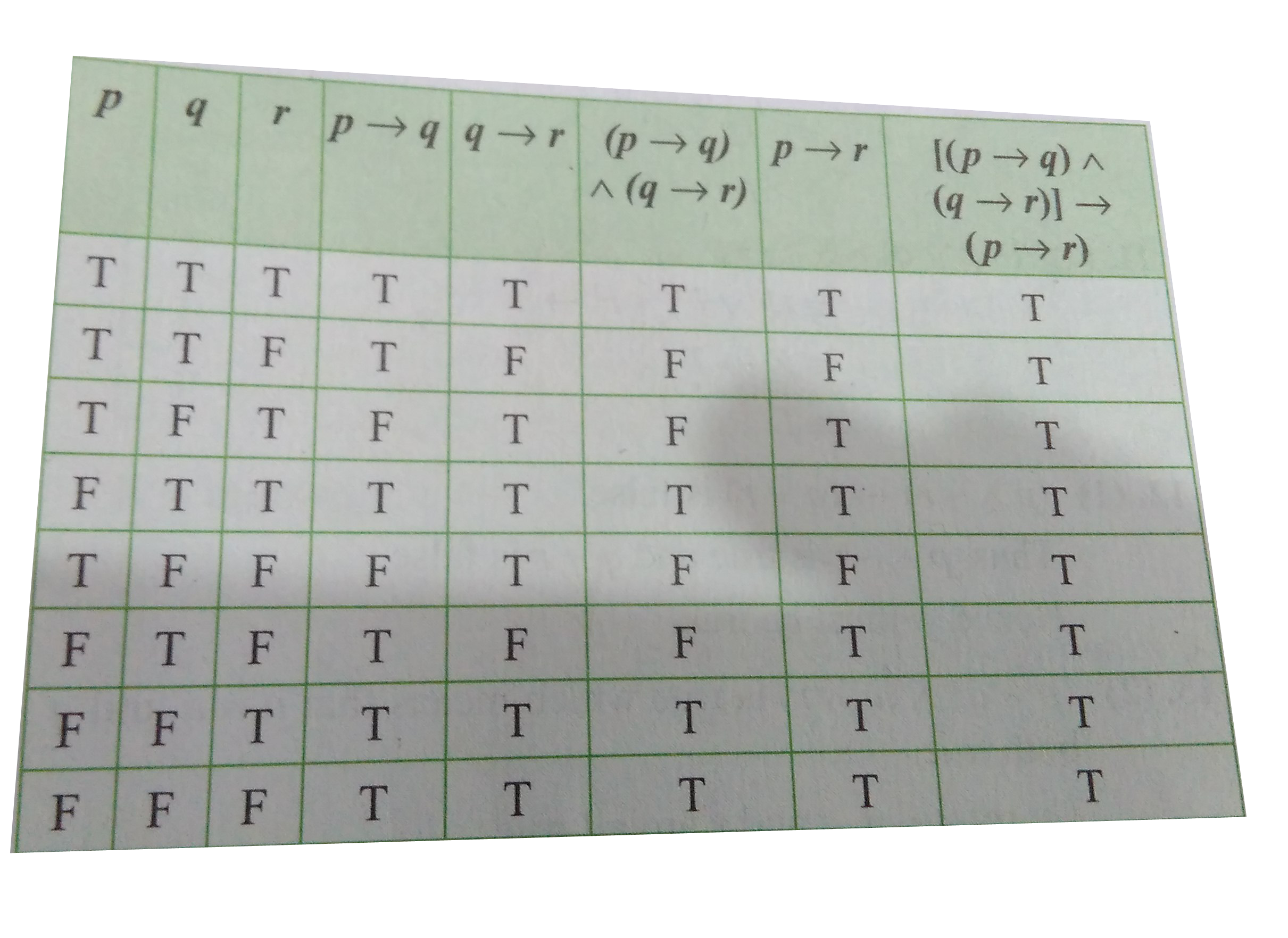
Play - Show that [(ptoq)^^(qto r)] to ( p to r)is a tautology
05:03
|
Playing Now - Prove that ~((~p)^^q) -=pvv(~q).
04:09
|
Play - prove that (p^^q) ^^~(pvvq) is a contradiction.
01:15
|
Play - Prove that ~(~pto ~q) -=~p ^^q
01:17
|
Play