A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
THREE-DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise MATRIX-MATCH TYPE|5 VideosView PlaylistTHREE-DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise INTEGER TYPE|10 VideosView PlaylistTHREE-DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise REASONING TYPE|10 VideosView PlaylistTHREE DIMENSIONAL GEOMETRY
CENGAGE PUBLICATION|Exercise All Questions|291 VideosView PlaylistTRIGONOMETRIC EQUATIONS
CENGAGE PUBLICATION|Exercise Archives (Numerical value type)|4 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-THREE-DIMENSIONAL GEOMETRY -LINKED COMPREHENSION TYPE
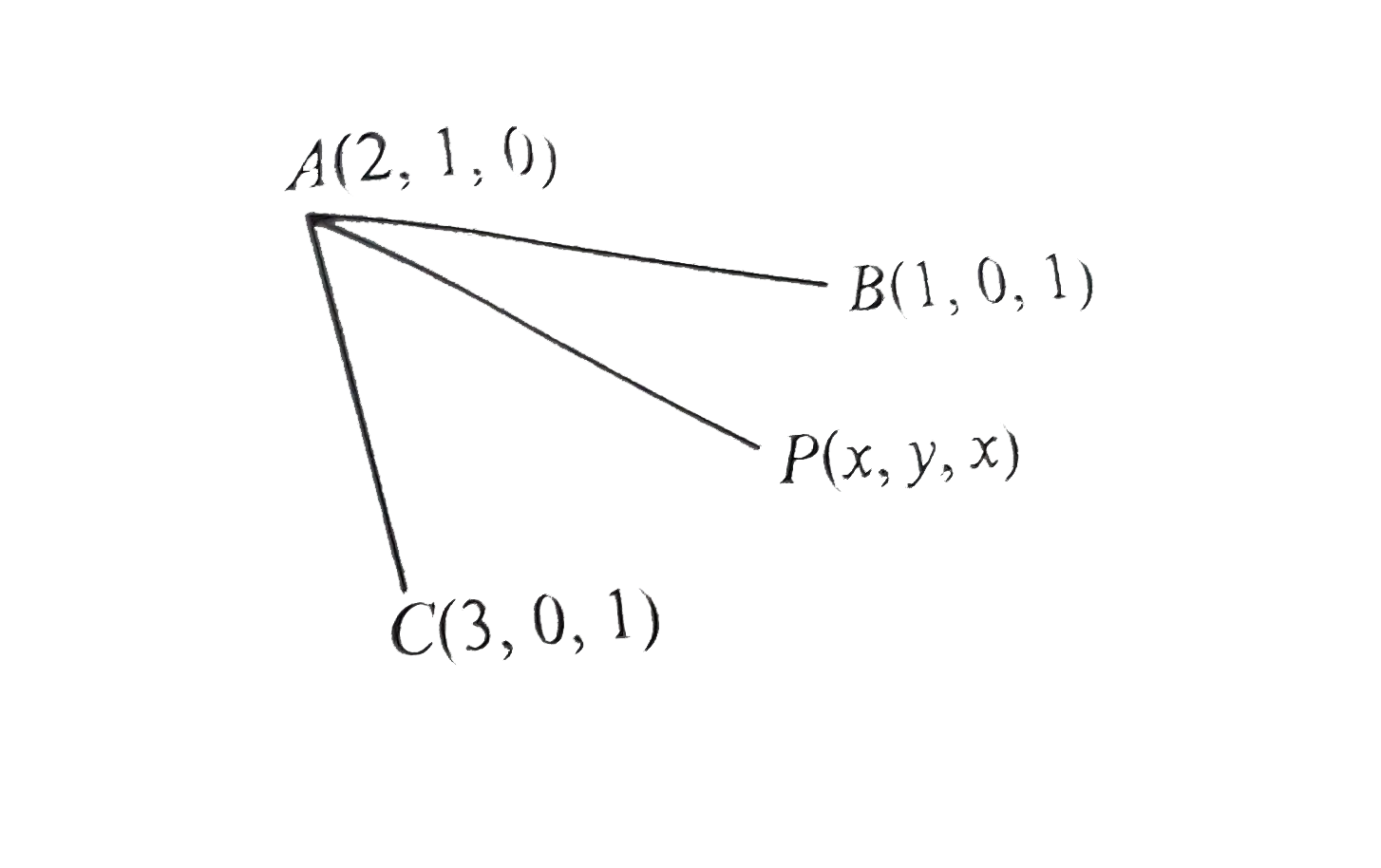
- Given four points A(2, 1, 0), B(1, 0, 1), C(3, 0, 1) and D(0, 0, 2). P...
02:39
|
Playing Now - Given four points A(2, 1, 0), B(1, 0, 1), C(3, 0, 1) and D(0, 0, 2). P...
02:39
|
Play - Given four points A(2, 1, 0), B(1, 0, 1), C(3, 0, 1) and D(0, 0, 2). P...
02:39
|
Play - A ray of light comes light comes along the line L = 0 and strikes the ...
03:32
|
Play - A ray of light comes along the line L = 0 and strikes the plane mirror...
05:27
|
Play - A ray of light comes along the line L = 0 and strikes the plane mirror...
14:42
|
Play - For what values of p and q the system of equations 2x+py+6z=8, x+2y+qz...
06:30
|
Play - For what values of p and q the system of equations 2x+py+6z=8, x+2y+qz...
06:30
|
Play - For what values of p and q the system of equations 2x+py+6z=8, x+2y+qz...
06:30
|
Play - Consider a plane x+y-z=1 and point A(1, 2, -3). A line L has the equat...
05:08
|
Play - Consider a plane x+y-z=1 and point A(1, 2, -3). A line L has the equat...
05:08
|
Play - Consider a plane x+y-z=1 and point A(1, 2, -3). A line L has the equat...
05:08
|
Play