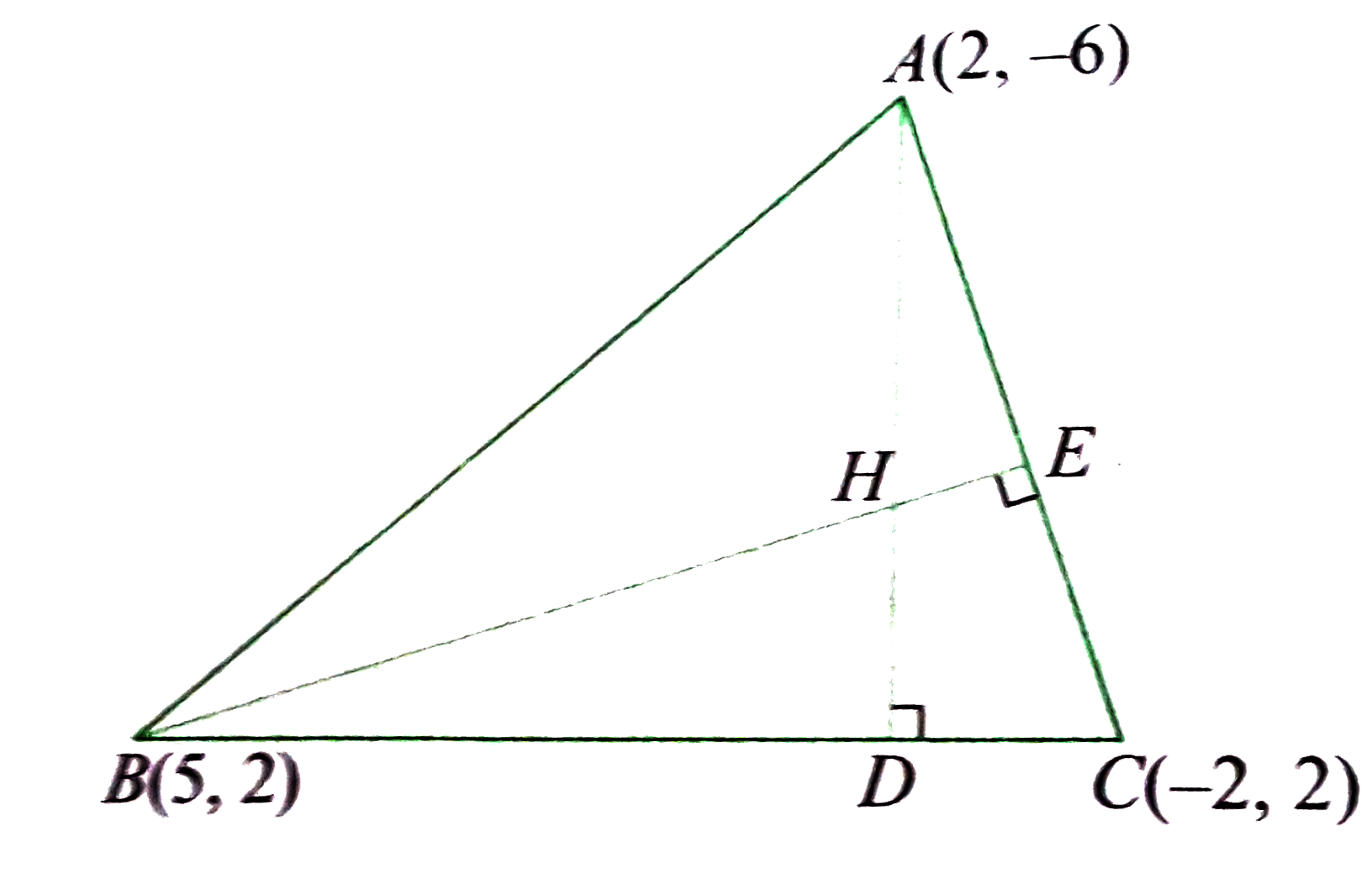
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
COORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Numerical value|12 VideosView PlaylistCOORDINATE SYSTEM
CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|2 VideosView PlaylistCROSS PRODUCTS
CENGAGE PUBLICATION|Exercise DPP 2.2|13 VideosView Playlist
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-COORDINATE SYSYEM -JEE Main
- The lines p(p^2+1)x-y+q=0 and (p^2+1)^2x+(p^2+1)y+2q=0 are perpendicul...
02:08
|
Play - If the line 2x + y = k passes through the point which divides the line...
05:06
|
Play - The number of points, having both co-ordinates as integers, that lie ...
03:48
|
Play - Let k be an integer such that the triangle with vertices (k ,-3k),(5...
07:00
|
Playing Now - If the orthocentre and centroid of a triangle are (-3, 5) and (3, 3) t...
06:00
|
Play - The straight line through a fixed point (2,3) intersects the coordinat...
03:34
|
Play