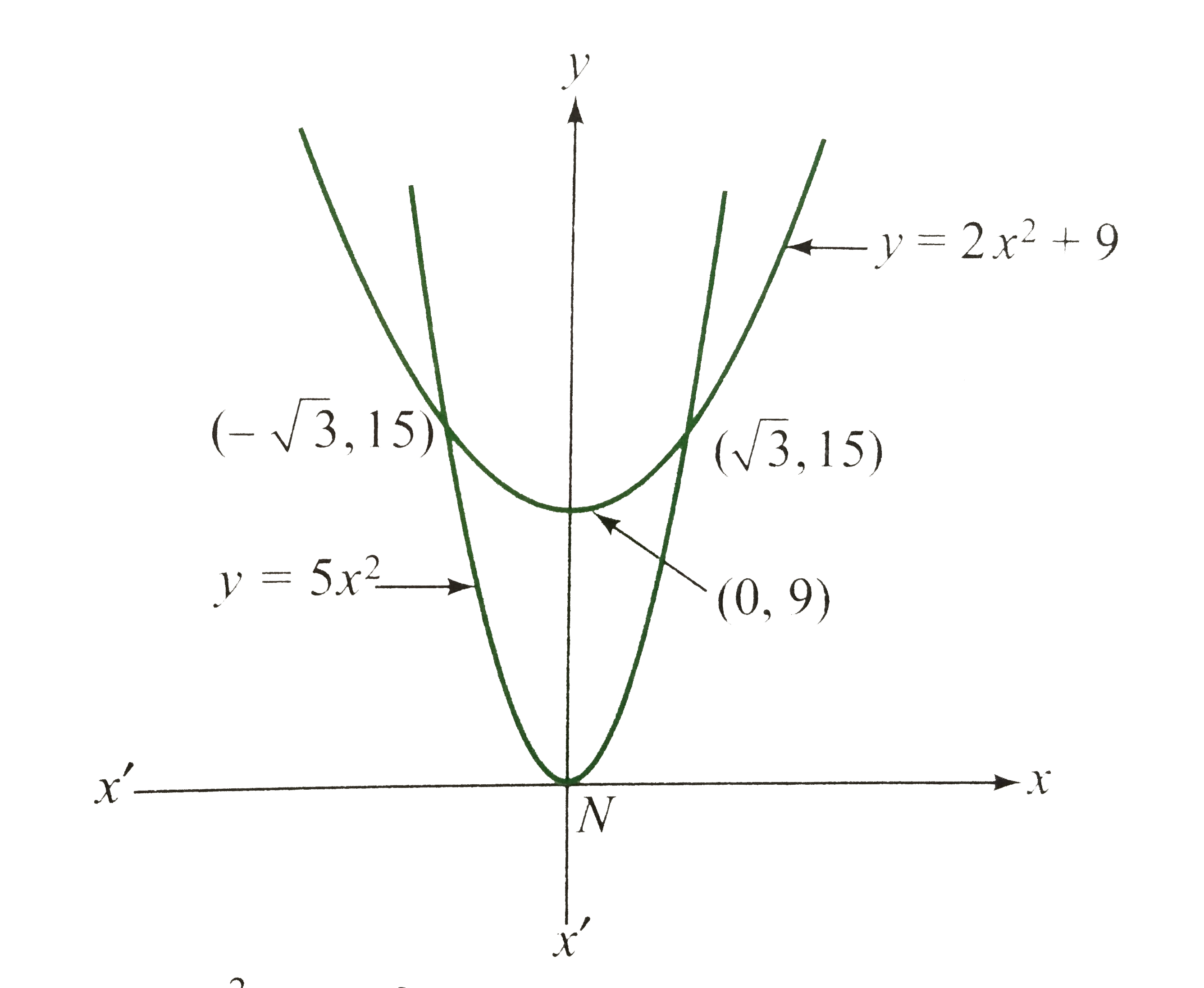Home
Class 12
MATHS
The area inside the parabola 5x^2-y=0 bu...

The area inside the parabola `5x^2-y=0` but outside the parabola `2x^2-y+9=0` is (a) `12sqrt(3)` sq units (b) `6sqrt(3)` sq units (c) `8sqrt(3)` sq units (d) `4sqrt(3)` sq units

A

`12sqrt(3)` sq. units

B

`6sqrt(3)` sq. units

C

`8sqrt(3)` sq. units

D

`4sqrt(3)` sq. units

Text Solution

Verified by Experts

The correct Answer is:
A

`"Given "5x^(2)-y=0" ...(1)"`
`"and "2x^(2)-y+9=0" ...(2)"`
`5x^(2)-(2x^(2)+9)=0`
`"or "3x^(2)=9 or x=-sqrt(3),sqrt(3)`
`therefore" Required area "=2int_(0)^(sqrt(3))((2x^(2)+9)-5x^(2))dx`
`=2int_(0)^(sqrt(3))(9-3x^(2))dx`
`=2[9x-x^(3)]_(0)^(sqrt(3))`
`=2[9sqrt(3)-3sqrt(3)]`
`=12sqrt(3)` sq. units
Promotional Banner

Topper's Solved these Questions

  • AREA

    CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|13 Videos

  • AREA

    CENGAGE PUBLICATION|Exercise Linkded Comprehension Type|21 Videos

  • AREA

    CENGAGE PUBLICATION|Exercise Concept Application Exercise 9.3|7 Videos

  • APPLICATIONS OF DERIVATIVES

    CENGAGE PUBLICATION|Exercise Subjective Type|2 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

Similar Questions

Explore conceptually related problems

If the area inside the parabola 5x^(2) -y=0 but outside the parabola 2x^(2) -y+ 9 =0 is 2K sqrt 3 sq . Units then the value of K is equal to-

The area bounded by the parabolas y=(x+1)^2 and y=(x-1)^2a n dy=(x-1)^2 and the line y=1/4 is (a)4 sq. units (b) 1/6 sq. units 4/3 sq. units (d) 1/3 sq. units

The area enclosed by 2|x|+3|y|lt=6 is (a) 3 sq. units (b) 4 sq. units 12 sq. units (d) 24 sq. units

The area bounded by the curves y=|x|-1a n dy=-|x|+1 is 1 sq. units (b) 2 sq. units 2sqrt(2) sq. units (d) 4 sq. units

The area bounded by the curves y=sqrt(x),2y+3=x , and x-axis in the 1st quadrant is (A) 18 sq. units (B) (27)/4 sq.units (C) 4/3 sq.units (D) 9 sq. units

Area of the triangle formed by the line x+y=3 and the angle bisectors of the pairs of straight lines x^2-y^2+2y=1 is (a) 2 sq units (b) 4 sq units (c) 6 sq units (d) 8 sq units

The area bounded by the curves y=log_e x and y=(log_e x)^2 is (A) e-2 sq. units (B) 3-e sq. units (C) e sq. units (D) e-1 sq. units

The area bounded by y=sec^-1 x,y=cosec^-1x, and line x-1=0 is (a) log(3+2sqrt2)-pi/2 sq. units (b) pi/2-log(3+2sqrt2) sq. units (c) pi-(log)_e 3 sq. units (d) non of these

A rhombus is inscribed in the region common to the two circles x^2+y^2-4x-12=0 and x^2+y^2+4x-12=0 with two of its vertices on the line joining the centers of the circles. The are of the rhombus is (A) 8sqrt(3) sq.units (B) 4sqrt(3) sq.units (C) 6sqrt(3) sq.units (D) none of these

Let f(x)=min (x+1,sqrt(1-x)) for all xlt=1. Then the area bounded by y=f(x) and the x-axis is (a) 7/3 sq units (b) 1/6 sq units (c) (11)/6 sq units (d) 7/6 sq units

CENGAGE PUBLICATION-AREA-Exercises - Single Correct Answer Type
  1. The positive valu of the parameter 'k' for which the area of the figu...

    Text Solution

    |

  2. The area bounded by the curve y=x(1-log(e)x) and x-axis is (a) (e^(2...

    Text Solution

    |

  3. The area inside the parabola 5x^2-y=0 but outside the parabola 2x^2-y+...

    Text Solution

    |

  4. Area enclosed between the curves |y|=1-x^2 and x^2+y^2=1 is (a) (3pi-8...

    Text Solution

    |

  5. If An is the area bounded by y=x and y=x^n ,n in \mathbb{N} ,then A2 A...

    Text Solution

    |

  6. The area of the region is 1st quadrant bounded by the y-axis, y=(x)/(4...

    Text Solution

    |

  7. The area of the closed figure bounded by y=(x^2)/2-2x+2 and the tangen...

    Text Solution

    |

  8. The area of the region bounded by x^(2)+y^(2)-2x-3=0 and y=|x|+1 is

    Text Solution

    |

  9. The area enclosed by the curve y=sqrt(4-x^2),ygeqsqrt(2)sin((xpi)/(2sq...

    Text Solution

    |

  10. The area bounded by the curve y^(2)(2-x)=x^(3) and x=2 is

    Text Solution

    |

  11. The area bounded by the curves y=(log)e xa n dy=((log)e x)^2 is

    Text Solution

    |

  12. The area bounded by y = 3-|3-x| and y=6/(|x+1|) is

    Text Solution

    |

  13. The area enclosed between the curves y=(log)e(x+e),x=(log)e(1/y), and ...

    Text Solution

    |

  14. Find the area enclosed the curve y=sin x and the X-axis between x=0 an...

    Text Solution

    |

  15. The area bounded by y=x^(2),y=[x+1], 0 le x le 2 and the y-axis is whe...

    Text Solution

    |

  16. The area of the figure bounded by the parabola (y-2)^2=x-1, the tangen...

    Text Solution

    |

  17. The area bounded by the curves y=x e^x ,y=x e^(-x) and the line x=1 is...

    Text Solution

    |

  18. The area of the region whose boundaries are defined by the curves y=2 ...

    Text Solution

    |

  19. The area bounded by y=sec^(-1)x , y=cos e c^(-1)x , and line x-1=0 is ...

    Text Solution

    |

  20. The area bounded by the curve y=3/|x| and y+|2-x|=2 is

    Text Solution

    |