A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
AREA
CENGAGE PUBLICATION|Exercise Single Correct Answer Type|30 VideosView PlaylistAREA
CENGAGE PUBLICATION|Exercise Multiple Correct Answer Type|3 VideosView PlaylistAREA
CENGAGE PUBLICATION|Exercise Numerical Value Type|18 VideosView PlaylistAPPLICATIONS OF DERIVATIVES
CENGAGE PUBLICATION|Exercise Subjective Type|2 VideosView PlaylistBINOMIAL THEOREM
CENGAGE PUBLICATION|Exercise Comprehension|11 VideosView Playlist
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-AREA-Archives
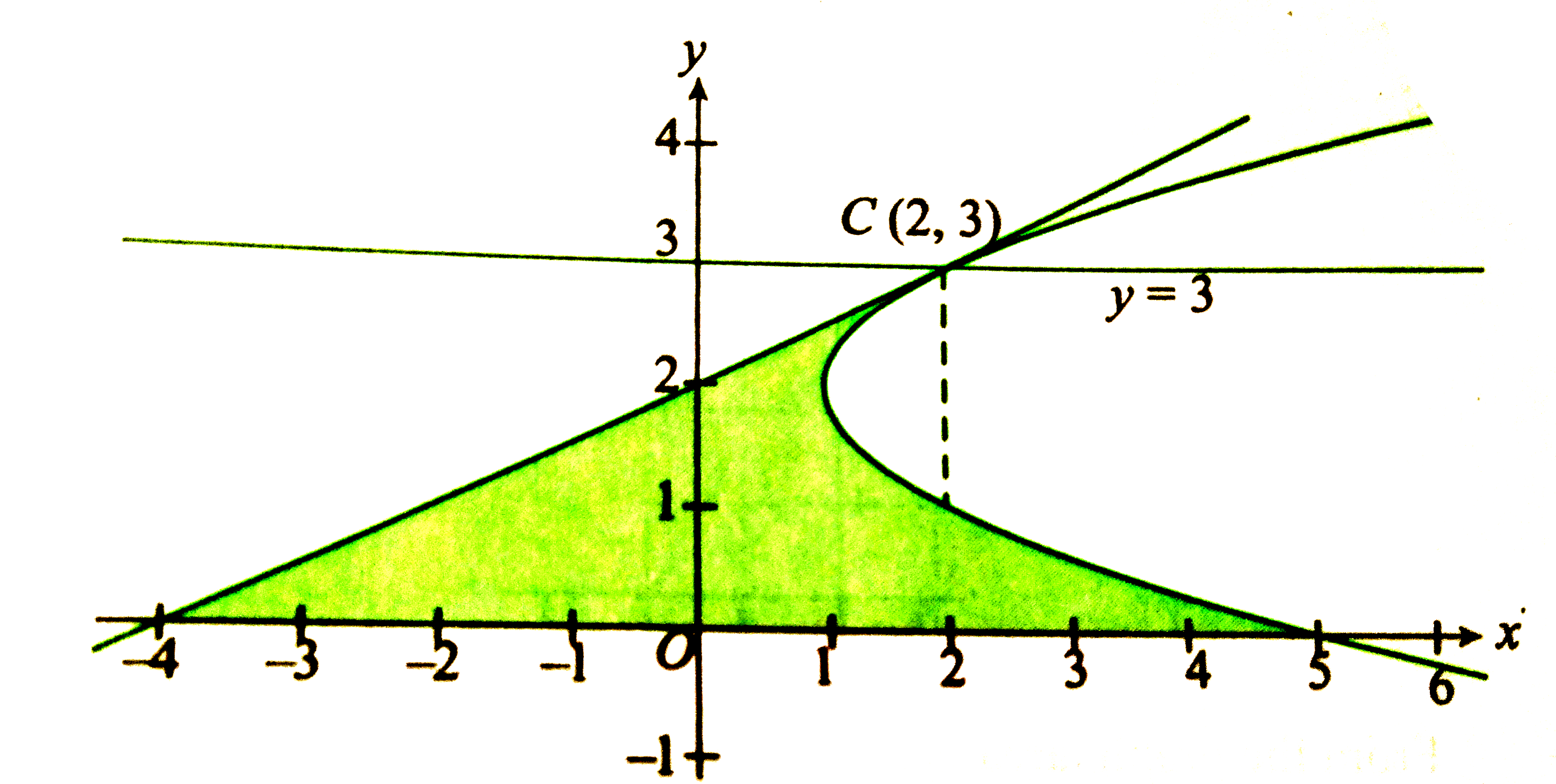
- The area of the figure bounded by the parabola (y-2)^2=x-1, the tangen...
14:01
|
Playing Now - The area bounded by the curves y=cosx and y=sinx between the ordinates...
03:12
|
Play - The area of the region enclosed by the curve y=x, x=e,y=1/x and the po...
02:42
|
Play - The area bounded by the parabolas y=4x^(2), y=(x^(2))/(9) and the stra...
05:42
|
Play - The area bounded by the curves y=sqrt(x),2y+3=x , and x-axis in the 1s...
07:40
|
Play - The area of the region described by A = {(x,y) : x^2 + y^2 lt= 1and y^...
05:18
|
Play - The area (in sq. units) of the region described by {x,y):y^(2)le2x and...
07:02
|
Play - The area (in sq units) of the region {(x, y) : y^2 gt= 2x and x^2 + y^...
04:46
|
Play - The area (in sq units) of the region bounded by the curve y = sqrtx an...
05:42
|
Play - Let g(x)=cos^2 x,f(x)=sqrtx and alpha,beta (alpha < beta) be the roo...
05:09
|
Play