Home
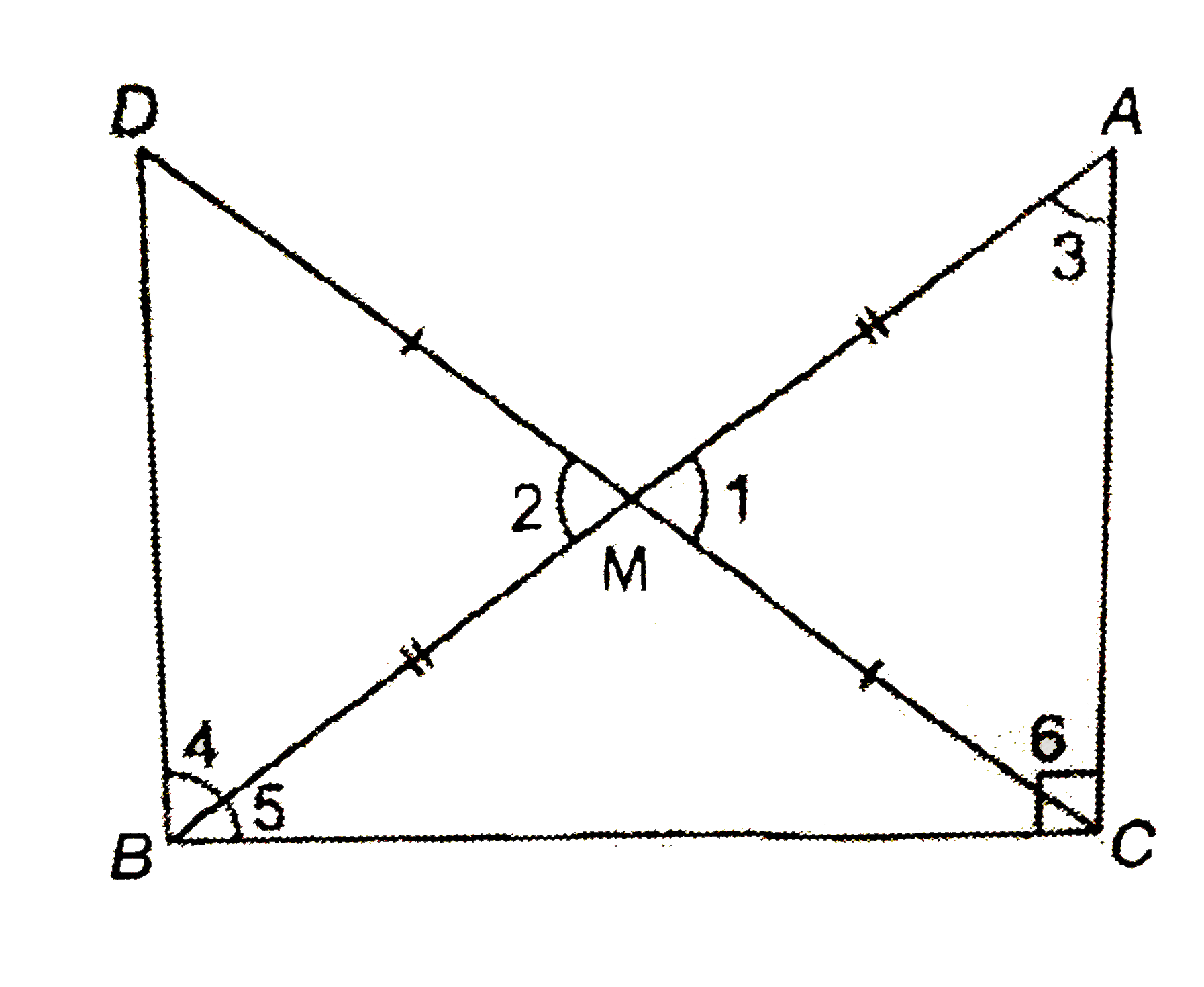
Class 8
MATHS
In right triangle ABC, right angle at C,...

In right triangle ABC, right angle at C, M is the mid-point of the hydrotenuse AB. C is joined to M and produced to a point D such that `DM=CM`. Point D is joined to point B. Show that
(i) `DeltaAMC cong DeltaBMD` (ii) `angleDBC=angleACB`
(iii) `DeltaDBC cong DeltaACB` (iv) `CM=1/2 AB`

A

ASA

B

RHS

C

SSS

D

SAS

Text Solution

Verified by Experts

The correct Answer is:
D
Promotional Banner

Topper's Solved these Questions

  • TRIANGLES

    S CHAND IIT JEE FOUNDATION|Exercise Question Bank|30 Videos

  • TIME AND WORK

    S CHAND IIT JEE FOUNDATION|Exercise Self Assessment Sheet - 20|10 Videos

  • TRIGONOMETRICAL RATIOS

    S CHAND IIT JEE FOUNDATION|Exercise Self Assessment Sheet - 40|1 Videos

Similar Questions

Explore conceptually related problems

In right triangle ABC, right angled at C, Mis the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that DeltaAMC~=DeltaBMD

In right triangle ABC, right angled at C, Mis the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that DeltaDBC~=DeltaACB

In right triangle ABC, right angled at C, Mis the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that angleDBC is right angle.

In right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that D M\ =\ C M . Point D is joined to point B (see Fig. 7.23). Show that: (i) DeltaA M C~=DeltaB M D (ii) /_DBC is a right angle (iii) Δ DBC ≅ Δ ACB (iv) CM =1/2 AB

In right triangle A B C , right angle at C , M is the mid-point of the hypotenuse A Bdot C is jointed to M and produced to a point D such that D M=C Ddot Point D is joined to point Bdot Show that A M C~= B M D (ii) /_D B C=/_A C B D B C~= A C B (iii) C M=1/2A B

If D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=(1)/(2)AC

In a right ABC right-angled at C, if D is the mid-point of BC, prove that BC^(2)=4(AD^(2)-AC^(2))

The following figure shows a triangle ABC in which Ab = AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that : (i) AM = AN (ii) DeltaAMC cong DeltaANB (iii) BN=CM (iv) DeltaBMC cong DeltaCNB