Home
Class 12
MATHS
The figure shows a right triangle with i...

The figure shows a right triangle with its hypotenuse `OB` along the `y`-axis and its vertex `A` on the parabola `y=x^(2)`.

Let `h` represents the length of the hypotenuse which depends on the `x`-coordinate of the point `A`. The value of `lim_(t to o (h)` is equal to

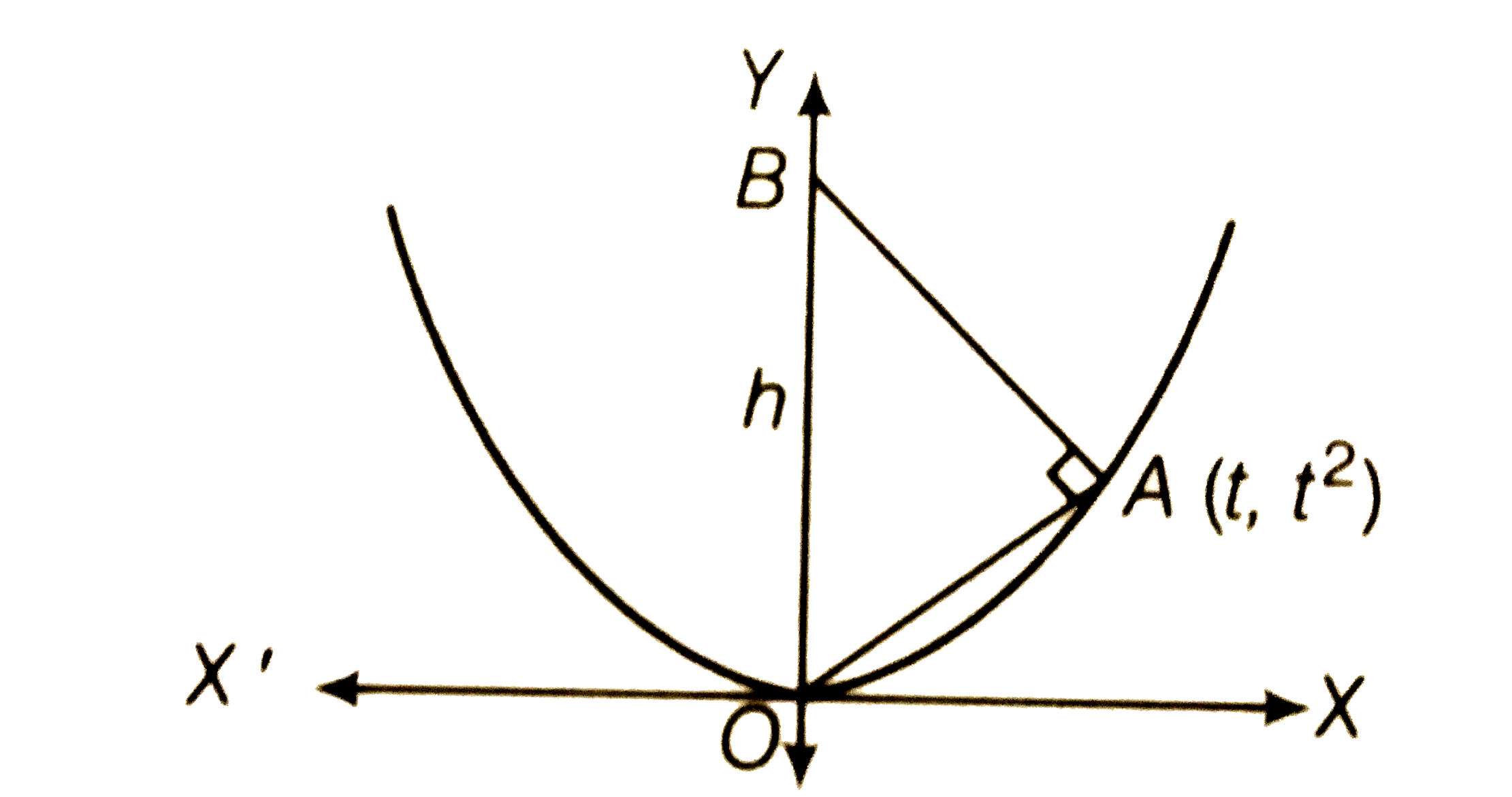
Text Solution

Verified by Experts

The correct Answer is:
1
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • MONOTONICITY MAXIMA AND MINIMA

    ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|31 Videos

  • MONOTONICITY MAXIMA AND MINIMA

    ARIHANT MATHS|Exercise Exercise (Single Integer Answer Type Questions)|11 Videos

  • MATRICES

    ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|49 Videos

  • PAIR OF STRAIGHT LINES

    ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|2 Videos

Similar Questions

Explore conceptually related problems

If the vertex of the parabola y=x^(2) -8x+c lies on x-axis, then the value of c, is

Find the coordinates of a point on the x-axis whose distance from the line 3x-4y-2=0 is equal to 2.

The parabola having its focus at (3,2) and directrix along the Y-axis has its vertex at

An equilateral triangle is inscribed in the parabola y^(2)=4ax whose vertex is at the vertex of the parabola .Find the length of its side.

Find the area of the triangle formed by the lines joining the vertex of the parabola x^2 = 12y to the ends of its latus rectum.

Find the area of the triangle formed by the lines joining the vertex of the parabola x^2 = 12y to the ends of its latus rectum.

Find the locus of the middle points of the chords of the parabola y^2=4a x which subtend a right angle at the vertex of the parabola.

Find the area of the triangle formed by the lines joining the vertex of the parabola x^2= 12y to the ends of its latus-rectum.

If the parabola y^2=4a x\ passes through the point (3,2) then find the length of its latus rectum.

A curve is represented parametrically by the equations x=t+e^(at) and y=-t +e^(at), t in R and a gt 0 . If the curve touches the axis of x at the point A, then the coordinates of the point A are

Home
Profile