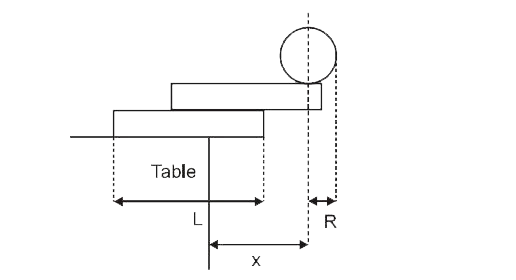
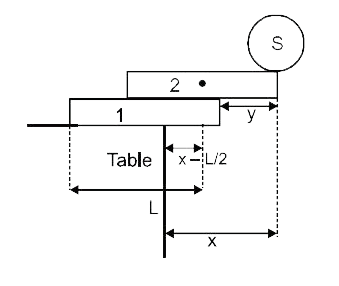
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
QUESTION PAPER 2013
KVPY PREVIOUS YEAR|Exercise PART-I ( PHYSICS)|20 VideosQUESTION PAPER 2013
KVPY PREVIOUS YEAR|Exercise PART-II ( PHYSICS)|10 VideosQUESTION PAPER 2013
KVPY PREVIOUS YEAR|Exercise PART-II ( PHYSICS)|10 VideosMOCK TEST 9
KVPY PREVIOUS YEAR|Exercise EXERCISE|19 VideosQUESTION PAPER 2020
KVPY PREVIOUS YEAR|Exercise PART-I : PHYSICS |50 Videos
Similar Questions
Explore conceptually related problems
KVPY PREVIOUS YEAR-QUESTION PAPER 2013-PART-II (PHYSICS)
- Two identical uniform rectangular blocks (with longest side L) and a s...
Text Solution
|
- Two skaters P and Q are skating towards each other. Skater P throws a ...
Text Solution
|
- A 10.0 W electrical heater is used to heat a container filled with 0.5...
Text Solution
|
- A ray of light incident on a transparent sphere at an angle pi//4 and ...
Text Solution
|
- An electron with an initial speed of 4.0 xx 10^6 ms^(-1) is brought t...
Text Solution
|