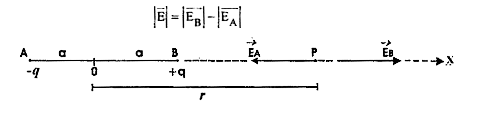Text Solution
Verified by Experts
|
Topper's Solved these Questions
ELECTRIC FIELD
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS |10 VideosView PlaylistELECTRIC FIELD
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS (MOST EXPECTED QUESTIONS)|4 VideosView PlaylistELECTRIC FIELD
BETTER CHOICE PUBLICATION|Exercise SHORT ANSWER TYPE QUESTIONS |7 VideosView PlaylistELECTRIC CURRENT, RESISTANCE AND E.M.F.
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED QUESTIONS |14 VideosView PlaylistELECTRICAL DEVICES
BETTER CHOICE PUBLICATION|Exercise (MOST EXPECTED QUESTIONS 2 MARK)|2 VideosView Playlist
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-ELECTRIC FIELD-LONG ANSWER TYPE QUESTIONS
- Derive an expression for electric field intensity at a distance r from...
05:01
|
Play - Derive an expression for the electric potential at a point along the a...
03:13
|
Play - Define electric fied intensity and derive an expression for it at a po...
05:06
|
Playing Now - What is the direction of electric field due to an electric dipole at a...
02:06
|
Play - Define electric fied intensity and derive an expression for it at a po...
05:06
|
Play - Derive an expression for the torque acting on an electric dipole suspe...
04:53
|
Play - Which physical quantity has its SI unit(1) Cm (2) N/C.
02:23
|
Play - Two point charges q and -q is placed at a distance 2a apart.Calculate ...
06:58
|
Play - Two point charges q and-q are placed at a distance 2a part. Calculate ...
05:21
|
Play