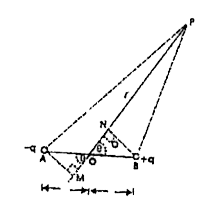
Text Solution
Verified by Experts
|
Topper's Solved these Questions
ELECTROSTATIC POTENTIAL
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS|16 VideosView PlaylistELECTROSTATIC POTENTIAL
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED QUESTIONS |7 VideosView PlaylistELECTROSTATIC POTENTIAL
BETTER CHOICE PUBLICATION|Exercise SHORT ANSWERTYPE QUESTIONS (2 Marks Questions)|9 VideosView PlaylistELECTRONIC DEVICES SOLIDS
BETTER CHOICE PUBLICATION|Exercise Most Expected Questions|9 VideosView PlaylistFORCE ON A CHARGE
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS |14 VideosView Playlist
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-ELECTROSTATIC POTENTIAL-LONG ANSWERTYPE QUESTIONS (5/6 Marks Questions)
- Define electric potential. What is the SI unit of potential? Obtain an...
03:43
|
Play - Show that work done in moving an electric charge between any two point...
03:56
|
Play - Define potential difference between two points in an electrostatic fie...
07:04
|
Play - Give the physical meaning of electrostatic potential?
03:27
|
Play - Obtain an expression for potential energy of the configuration of thr...
04:59
|
Play - What is electric potential enerrgy due to a system of charges? Derive ...
05:32
|
Play - What is the direction of electric field at a point on the equitorial l...
02:41
|
Playing Now - Show mathematically that the potential at a point on the equitorial li...
01:56
|
Play