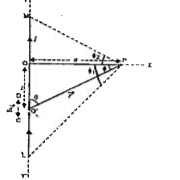
Text Solution
Verified by Experts
|
Topper's Solved these Questions
MAGNETIC EFFECTS OF CURRENT
BETTER CHOICE PUBLICATION|Exercise NUMERICALS PROBLEMS |3 VideosView PlaylistMAGNETIC EFFECTS OF CURRENT
BETTER CHOICE PUBLICATION|Exercise SHORT ANSWER TYPE QUESTIONS|4 VideosView PlaylistMAGNETIC DIPOLES AND EARTH'S MAGNETISM
BETTER CHOICE PUBLICATION|Exercise Most Expected Questions|8 VideosView PlaylistNUCLEAR REACTIONS
BETTER CHOICE PUBLICATION|Exercise Numerical Problems|9 VideosView Playlist
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-MAGNETIC EFFECTS OF CURRENT-LONG ANSWER TYPE QUESTIONS
- Using Ampere's circuital law, derive an expression for the magnetic fi...
02:51
|
Play - Using Ampere's circuital law, derive an expression for the magnetic fi...
02:51
|
Play - Derive an expression for magnetic field at the centre of circular curr...
04:30
|
Play - The magnetic field at a point due to a current carrying conductor is d...
01:17
|
Play - State the Biot-Savart's law for the magnetic field due to a current ca...
07:09
|
Play - Derive an expression for magnetic field at the centre of circular curr...
04:30
|
Play - Derive an expression for magnetic field at the centre of circular curr...
04:30
|
Play - Write expression for the magnetic flux density at a point due to a cur...
02:22
|
Play - Write expression for the magnetic flux density at a point due to a cur...
05:05
|
Playing Now - State Ampere's circuital law. By using it derive an expression for mag...
05:57
|
Play - State Ampere's circuital law. By using it derive an expression for mag...
05:57
|
Play - State Ampere's circuital law. By using it derive an expression for mag...
05:57
|
Play - State the rule that is used to find the direction of field acting at a...
01:18
|
Play - Using Ampere's circuital theorem, calculate the magnetic field due to ...
02:03
|
Play - What is Maxwell's right hand thumb rule?
01:11
|
Play - State Biot-Savart law. Using Biot-Savart law find the magnitude and di...
05:01
|
Play